Caching

SAT, , ,

“Representation is the essence of programming”
Frederic P. Brooks Jr., “The Mythical Man-month”

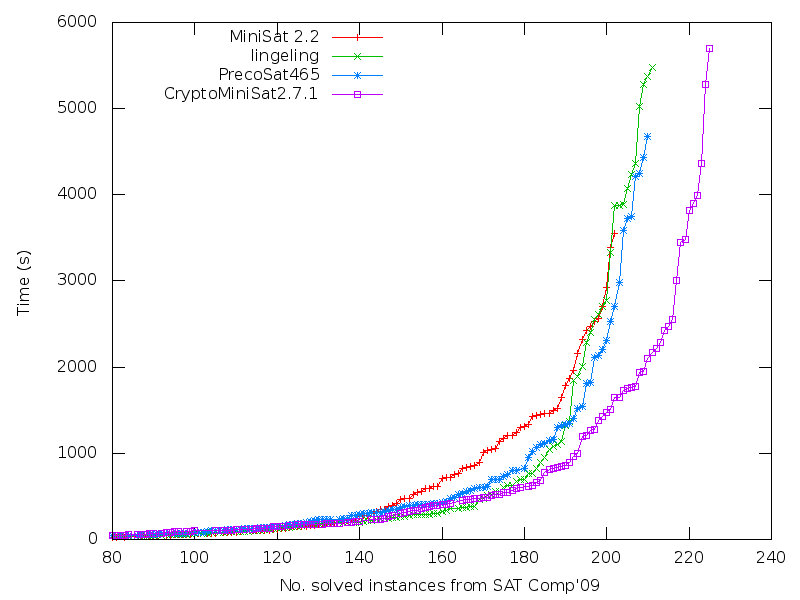
Looking through the literature on SAT solvers, it is rare to find any algorithm that uses a form of time-memory trade-off. In fact, it is rare to find any algorithm that uses too much memory. This also shows up in practice, as it’s rare to find a SAT solver using too much memory. This translates to the following: if a SAT solver can in an effective way utilize the typically abundant memory, that SAT solver will have an advantage. Based on this logic, I think CryptoMiniSat is doing good.

What I have realised is that it’s great to know all the literals we can reach from any given literal. Let me explain. Let’s say we have a look at literal “v1”, i.e. “v1 = true”. We propagate this literal as usual, and we reach a set of literals that are implied. For example, we reach “v2, v3, -v4”. This knowledge is regularly computed by modern SAT solvers, but is also quickly thrown away. I advocate keeping this, and here is why. There are a number of very interesting things we can do with these, three of which I have found useful.

Number one. This is the best, and the least obvious one. The algorithm used for computing equivalent literals (i.e. “v1 = -v2” or “v1 = v4”) is a variation of Tarjan’s algorithm for finding strongly connected components (SCC). This algorithm requires a set of binary clauses such as “-v1 v2” and “v1 -v2” as input to find equivalent literals, in the example case “v1 = -v2”. The most obvious way to “feed” this algorithm with information is to give it all the binary clauses we have. But that misses out on all the binary clauses that are not directly apparent in the problem, but  could be derived from the problem. For example, if “-v1 -v4” was not directly in the problem, SCC cannot find the equivalence “v1 = v4”. Naturally, by using our cache, we can be sure that “-v1 -v4” is part of the problem (since “v1” propagates “-v4”). So, using this cache, we can substantially increase the power of SCC. More equivalent literals lead to less variables, and an overall faster solving.

Number two. Clause vivification is a method to make the original clauses of the problem shorter. It’s a relatively simple algorithm that enqueues the literals in the clauses one-by-one and checks if their propagation leads to a conflict. If so, then the clause can be shortened. With the cache, we can do something similar, though less powerful in terms of reasoning power, but far more effective in terms of speed. The trick is to simply try every single literal in the clause: if a literal propagates the inverse of another literal in the clause, we can remove it. For example, if the clause is “a b -c”, and in the cache for “b” there is “f,g,h,j,-c”, then we know that conceptually there exists a clause “-b -c”, which means we can now remove “b” from the original clause, using the the self-subsuming resolution rule. This form of vivification is, although technically less strong than normal vivification, is typically 50-100x faster than normal vivification and is almost as powerful. This kind of speed advantage means it can essentially be carried out without (time) penalty.

Number three. When generating conflict clauses, MiniSat-type conflict minimisation has now become commonplace. This uses the clauses involved in the conflict to carry out self-subsuming resolution on the conflict clause generated. Just as with clause vivification, we can use our cache to carry out self-subsuming resolution with the (conceptually binary) clauses stored in the cache. This is not much different from clause vivification, but it allows us to do simplification in the middle of a restart, instead of patiently waiting for the restart to end. Furthermore, it can uncover that certain learnt clauses can become binary, thus alleviating the problem of cleaning “useless” learnt clauses that could have become binary through, e.g. clause vivification.

I am aware that all the above three could be carried out without a cache — in fact, CryptoMiniSat could do (and most of the time did) all of the above without it. The advantage of having the cache is speed: things that used to take immense amounts of time can now be done really fast. However, what interests me the most in this cache, is the new uses that will come of it. I was originally only aware of number (3), then when I realised (1), I dived deep and realised that (2) can be done. I think more uses will eventually emerge.

The Cathedral

SAT,

Cathedral of Transfiguration in Habarovsk (picture credit: paukrus)

Last week I visited Micosoft Reasearch in Cambridge, where I gave a talk on SAT solvers, Grobner basis algorithms, and Cryptography. It was nice to visit Microsoft, and in particular I enjoyed seeing how “the cathedral” works. The kind of software development carried out at Microsoft and almost all large software companies is called the cathedral model due to the book “The Mythical Man-Month“. It’s a very interesting book that talks about how software (and in particular, a “Programming Systems Product”) is developed. All Windows variants, and e.g. the IBM System/360 fall into the category of programming systems products: they are all tested, documented, extensible, have predefined inputs and outputs, come with predefined interfaces, etc. The development of these software is called the cathedral model simply because that’s the example the book uses, and it got stuck in the literature.

I have been developing CryptoMiniSat for quite some while now, and I must say it is exceedingly difficult to create a programming systems product — CryptoMiniSat doesn’t even scratch the surface of the requirements, but then almost no SAT solver does — maybe SAT4J is the sole exception. Documentation is usually scarce, and even though I have added a lot, it’s still not enough. The input is rarely checked for sanity, and resource needs are usually just ignored: if memory is not enough, then the program will probably just crash; don’t expect graceful degradation.

As for Microsoft, I must say I was pretty impressed. It’s a nice building, with large offices, free tea/coffee/orange juice, filled with some very kind and very bright people. The audience was astonishingly good too, asking questions when they felt like they haven’t understood something, instead of just getting disinterested and e.g. browsing email. All in all, it was very interesting to visit the place, though I still feel more inclined to release my code as Free Software ;)

Implicit binary clauses

SAT, ,

I have lately been trying to get CryptoMiniSat to use implicit binary clauses. The idea is that since binary clauses are very trivial (just two literals), and they don’t really need to keep state (like clause activity), they don’t really need to be stored at a separate location. Instead, they can be stored directly in the watchlists. There are a number of advantages and disadvantages that come with this approach.

The main advantage is a notable reduction of memory usage and memory fragmentation. The first is obvious: since we don’t allocate space for binary clauses separately, the memory usage of the program should go down. This is especially true since SAT problems usually contain a huge number of binary clauses. The secondary benefit, that of reduced memory fragmentation is not really that much of an advantage if someone uses, e.g. the boost pool library.

The disadvantages are mainly twofold. Firstly, bugs are very difficult to find. Since there is not one central database of binary clauses (as before), it becomes difficult to check the consistency of the watchlists. However, if inconsistencies creep in, then the solution found by the SAT solver could be wrong. Worst of all, consistency is difficult to keep, as binary clauses often need to be worked on by e.g. subsumption, variable elimination, etc. The second biggest disadvatage is that if a new algorithm comes up that needs a database of binary clauses, this database would need to be re-built every time to run that algorithm, which can be very costly in terms of time.

All in all, it took me about 1 day to implement implicit binary clauses, and about 3 days to debug it. Surprisingly, it came with some very positive side-effects. Firstly, the debugging session took out some very long-standing bugs in CryptoMiniSat. Secondly, since binary clauses represent most clauses in typical SAT problems, and since binary clauses cannot be subsumed by anything other than binary clauses, the subsumption algorithm has been notably speeded up and its memory usage has been reduced. The worst part of using implicit binary clauses has been the fact that I can no longer use binary clause-sorting to find binary xor clauses, and I must resort back to Tarjan’s strongly connected component finding algorithm. This algorithm is algorithmically faster (only O(V+E) versus O(n*logn) ), but practically slower, since I need to carry it out repeatedly, and I cannot save state. Furthermore, I haven’t yet coded it down, so I am using boost’s graph algorithm, which means that I now have a dependency in CryptoMiniSat. This will eventually be corrected, but it is already causing some trouble.

In the meantime, I have been parallelising CryptoMiniSat. Funnily enough, it took me about 2 days in total to multi-thread CryptoMiniSat versus the 4 days it took to implement implicit binary clauses. Oh well.

Wasting cluster time

SAT,

Today marked the 100th cluster experiment I have conducted on the Grid’5000 cluster in Grenoble. The computers in this cluster are very powerful beasts, equipped with two Xeon Core i7-based processors, each with 4 cores for 8 cores in total with some impressive memory size and connectivity. The sad part is that since CryptoMiniSat is sequential software, I only use 1 core from the 8 total, since I cannot allow to have fluctuating test results due to memory-bandwidth problems when running multiple instances of the solver on the same physical computer. I have just counted, and using a very conservative estimate, I have wasted 41.8 years of  CPU core time to get CryptoMiniSat up to speed.

Was it worth wasting such immense amount of CPU core time to speed up a SAT solver? I think yes. First of all, I only used the cluster during night and during the weekends, when load was negligible. So, in a way I wasn’t wasting much apart from my own time launching the cluster experiments, collecting and analysing the results. Secondly, the feedback from the cluster immensely influenced my research and engineering decisions, and taught me many things regarding SAT. The best thing I have learnt is: never trust your intuitions when it comes to SAT. Secondly, good ideas on paper rarely turn out to be good ideas when first implemented, but with heavy tuning, they usually turn out to work well. Let me detail two examples.

Clause Vivification (I called it asymmetric branching) is a relatively simple example of why tuning is always necessary. This optimisation shortens clauses it is fed to, however, it is slow. The idea I used when tuning this optimisation is that the longest clauses are probably responsible for the slow solving and the long generated conflict clauses. So, I sort clauses according to size first, and then do clause vivification on the topmost (i.e. longest) clauses. Furthermore, I realised that enqueueing literals 2-by-2 on the stack (instead of enqueueing 1-by-1) saves significant time, and is almost as good as enqueueing them 1-by-1 — the difference is at most 1 literal in the final simplified clause.

A more complex example is that of speeding up self-subsuming resolution. The problem was that keeping all clauses attached in the watchlists slowed down self-subsuming resolution. However, the obvious solution of detaching all clauses and reattaching them after self-subs. resolution was incomplete, strangely enough. With multiple cluster experiments it became apparent that keeping clauses attached is important, because some propagations are made during the running of the algorithm, and propagating these (very few!) variables is crucial. The solution was to keep natively stored (2- and 3-long clauses) in the watchlists. These natively kept clauses don’t have pointers in the watchlists, and therefore their representation at the pointer’s location can be updated. The watchlists are therefore partially cleaned, then self-subsuming resolution is carried out, then the watchlists are fully cleaned and finally the watchlists are fully populated — not exactly a trivial algorithm, but it achieves both goals of fast and complete self-subsuming resolution.

—
Off-topic: For those who like contemporary art, here is a gem

CryptoMiniSat 2.7.1 released

SAT

It has been a long and winding road, but finally, CryptoMiniSat 2.7.1 has been released. The main additions relative to version 2.6.0 are:

  • Lots of documentation. I have added ~1’500 lines of comments to aid developers and user alike
  • Transitive on-the-fly self-subsuming resolution — an optimisation I have blogged about
  • Memory allocator has been fixed and updated
  • DIMACS parsing is now much better, which should allow for very interesting usage scenarios

Although the above list doesn’t seem to talk about performance, let me talk about it first. My personal point of view on performance is that different applications have different needs, so even if overall some solver is the best, it might not mean that it is the best for a particular application. I compared the performance of CryptoMiniSat 2.7.1 to the other mainline solvers, namely MiniSat 2.2, PrecoSat465, and lingeling. I ran the problem instances of the 2009 SAT Competition, with a timeout of 6’000 seconds on some powerful computers. The results are the following:

CryptoMiniSat could solve 225 problem instances (223 within SATComp’09 limits), and the second best solver, lingeling, could solve 211 (207 within SATComp’09 limits). Interestingly, both MiniSat 2.2 and lingeling were better than CryptoMiniSat 2.7.1 at low timeouts, and lingeling kept this advantage the longest, until ~500 seconds, above which CryptoMiniSat took over. Not being too fast at the beginning is a conscious choice by me, as I think it helps in the long run, though I might be wrong. There is much to be improved, and I hope that the immense amount of documentation added will help those willing to try to iron out these shortcomings.

As for the DIMACS parsing update, it basically allows to add information to clauses to distinguish between learnt and non-learnt clauses. This helps, because it is now possible to simply dump the learnt clauses at any moment during the search, and then re-start the search more-or-less where it was stopped. The command-line options for this are “–dumplearnts=FILENAME –maxdumplearnts=3” to dump, and “–alsoread=FILENAME” to re-read. This is currently quite a crude way of stopping-and-starting, but hopefully it will improve in the future.

All in all, I am quite happy about the new release. I have put lots of time into it, and I hope you will enjoy using it :)