Tag Archives: binary clauses

CryptoMinisat 3.1 released

Research, SAT, , , , ,

CryptoMinisat 3.1 has been released. The short changelog is:

$ git diff cryptoms-3.0 cryptoms-3.1 --shortstat
 84 files changed, 3079 insertions(+), 2751 deletions(-)

The changes made were threefold. First, memory usage has been greatly reduced. This is crucial, because memory usage was over 7GB on certain instances. Secondly, the implication cache wasn’t very well-used and an idea that came to my mind greatly improved performance on most problems. Finally, time limiting of some inprocessing techniques on certain types of problems has been improved.

Memory usage reduction

On instances that produced a lot of long learnt clauses the memory usage was very high. These learnt clauses were all automatically linked in to the occurrence list and consequently took large amounts of memory, sometimes up to 10GB. On other instances, the original clauses were too numerous and too large, so putting even them into the occurrence list was too much. On these instances, variable elimination is not carried out (or carried out only later, when enough original clauses have been removed/shortened). To debug some of these problems, I wrote a fuzzer that generates extremely large problems with many binary and many long clauses, it’s available here as “largefuzzer”. It’s actually quite nice with many-many binary clauses so it also can fuzz the problems encountered with probing of extremely weird and large instances.

Implied literal usage improvement

CryptoMiniSat uses implied literals, i.e. caches what literals were propagated by each literal during probing. It then re-uses this information to subsume and/or strengthen clauses. This is kind of similar to stamping though uses more memory. It is actually useful to have alongside stamping, and I now do both — propagating DFS that stamping requires is expensive though updating cache during DFS is just as easy as during quasi-BFS.

The trick I discovered while playing around with cached implied literals is that if literal L1 propagates L2 and also !L2 then that means there are conceptually two binary clauses in the solver (!L1, L2), (!L1, !L2), so !L1 is TRUE. This is of course trivial, but I never checked for this. The question most would raise is: why would L1 propagate both L2 and !L2 and not fail? The answer is kind of tricky, but very interesting. Let’s say at one point, L1 propagates L2 due to a learnt clause, but that learnt clause is then removed. A new learnt clause is then later learnt, and with that learnt clause in place, L1 propagates !L2. Now, without caching, this would be ignored. Caching memorizes past conceptual binary clauses and re-uses this information.

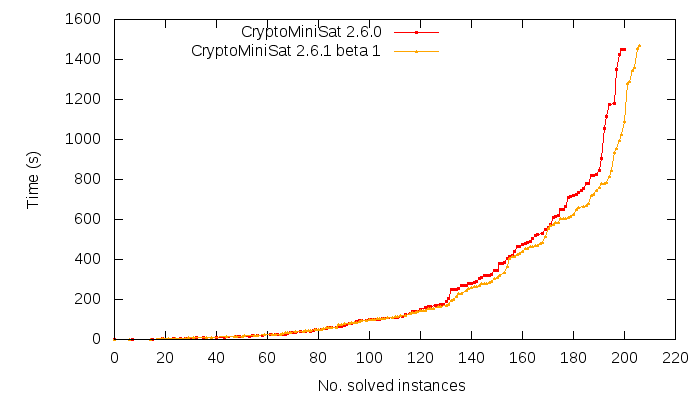
This is not an optimization that only looks good on paper, it is very good to have. With this one optimization, I gained 5 instances from the SAT Comp’09 instances with a 1000s timeout (196 solved -> 201 solved). I can’t right now imagine how this could be done with stamping effectively, but that doesn’t mean it’s not possible. Though, according to my experience, stamping doesn’t preserve that much information over time as it’s being updated (renumbered) frequently while the cache is only improved over time, never shrunk. A possibility would be to have more than one stamp system and round-robin selecting them. However that would mean that sorting of clauses (for shrinking) would need to be done more than once, and sorting them is already relatively expensive. I sometimes feel that what stamping gains in memory it looses on sorting (i.e. processing time) and lower coverage (re-numbering).

More precise time-limiting

Martin Maurer has been kind enough to file a lot of bug reports about probing and variable elimination taking too much time, sometimes upwards of 150s when they should take around 20-30s maximum. While investigating, it tuned out that the problem was very weird indeed. While trying to eliminate or probe one variable the time for that one variable took upwards of 100s. This was completely unexpected as the code only checked for timeouts on a per-variable basis. In the end, the code had to be improved to track time on an intra-variable basis in both systems. While at it, I also added intra-variable time-tracking to implicit clause subsumption and strengthening too. So, over-times should less prevalent from now on. As an interesting side-note, time-limiting on probing is now so fine-grained that a 32-bit unsigned integer would overflow within 15s if used as the time-tracker.

Failed literal probing and UIP

SAT, , ,

I have just realised that CryptoMiniSat, having won a number of medals, does one of the most basic things, failed literal probing, all wrong. Let me tell you why it’s all wrong. In essence, failed literal probing is trivial. We enqueue a fact, such as a, and then propagate it. If this fails, i.e. if two opposing facts such as g and -g are derived, we know that a cannot be true, so we set -a. Easy. Or maybe not so easy.

The devil is in the details, so let’s see how we derived both g and -g from a. Let’s assume that we have the following set of binary clauses:
-a V b
-b V c
-b V d
-d V e
-d V f
-e V g
-f V -g

which, from the point of view of a is best described as the graph:

Propagating "a", deriving both "g" and "-g"

The problem is, that if we only derive -a from this graph, we end up with only that one literal set, because -a doesn’t propagate anything on the clauses. This is quite sad, because, in fact, we could derive something stronger. From the graph it is evident that setting d would have failed: the graph would simply have its upper part cut away completely, but the lower part, including the derivation of both g and -g would still stand:

Deriving both "g" and "-g" from "d"

What is special about node d? Well, it’s where the 1st UIP, the first unique implication point, lies. And it is quite simple to see that -d is in fact the strongest thing we can derive from this graph. It’s much stronger than simply -a, because setting -d propagates on the clauses, giving -b,-a, setting three variables instead of one, including -a. An interesting observation is the following: deriving -b is the 2nd UIP, and deriving -a is the last UIP. In other words, at least in this most simple case, 1st UIP is in fact the strongest, and 2nd, 3rd.. last UIP are less strong in strict order.

Let me remark on one more thing about failed literal probing. Once failed literal probing has been done on literal x and it visited the node set N, there is no need to try to do failed literal probing on any nodes in N, since they cannot possibly fail. Although the failing of a literal can have consequences on the failing of other literals, if we ignore this side-effect, we could speed up failed literal probing by marking literals already visited, and only carrying out failed literal probing on ones that haven’t been marked. This is really trivial, but I haven’t been using it :S

I am quite sure that some advanced SAT solvers (such as lingeling) do all of the above things right. It’s probably only CryptoMiniSat that fails miserably :)

Note: there is a subtle bug with marking literals visited as “OK”. If two different subgraphs could fail, but we abort on the first one, then we might mark a literal OK when in fact it isn’t. It is therefore easiest not to mark any literals if the probe failed (which is very rare).

Caching

SAT, , ,

“Representation is the essence of programming”
Frederic P. Brooks Jr., “The Mythical Man-month”

Looking through the literature on SAT solvers, it is rare to find any algorithm that uses a form of time-memory trade-off. In fact, it is rare to find any algorithm that uses too much memory. This also shows up in practice, as it’s rare to find a SAT solver using too much memory. This translates to the following: if a SAT solver can in an effective way utilize the typically abundant memory, that SAT solver will have an advantage. Based on this logic, I think CryptoMiniSat is doing good.

What I have realised is that it’s great to know all the literals we can reach from any given literal. Let me explain. Let’s say we have a look at literal “v1”, i.e. “v1 = true”. We propagate this literal as usual, and we reach a set of literals that are implied. For example, we reach “v2, v3, -v4”. This knowledge is regularly computed by modern SAT solvers, but is also quickly thrown away. I advocate keeping this, and here is why. There are a number of very interesting things we can do with these, three of which I have found useful.

Number one. This is the best, and the least obvious one. The algorithm used for computing equivalent literals (i.e. “v1 = -v2” or “v1 = v4”) is a variation of Tarjan’s algorithm for finding strongly connected components (SCC). This algorithm requires a set of binary clauses such as “-v1 v2” and “v1 -v2” as input to find equivalent literals, in the example case “v1 = -v2”. The most obvious way to “feed” this algorithm with information is to give it all the binary clauses we have. But that misses out on all the binary clauses that are not directly apparent in the problem, but  could be derived from the problem. For example, if “-v1 -v4” was not directly in the problem, SCC cannot find the equivalence “v1 = v4”. Naturally, by using our cache, we can be sure that “-v1 -v4” is part of the problem (since “v1” propagates “-v4”). So, using this cache, we can substantially increase the power of SCC. More equivalent literals lead to less variables, and an overall faster solving.

Number two. Clause vivification is a method to make the original clauses of the problem shorter. It’s a relatively simple algorithm that enqueues the literals in the clauses one-by-one and checks if their propagation leads to a conflict. If so, then the clause can be shortened. With the cache, we can do something similar, though less powerful in terms of reasoning power, but far more effective in terms of speed. The trick is to simply try every single literal in the clause: if a literal propagates the inverse of another literal in the clause, we can remove it. For example, if the clause is “a b -c”, and in the cache for “b” there is “f,g,h,j,-c”, then we know that conceptually there exists a clause “-b -c”, which means we can now remove “b” from the original clause, using the the self-subsuming resolution rule. This form of vivification is, although technically less strong than normal vivification, is typically 50-100x faster than normal vivification and is almost as powerful. This kind of speed advantage means it can essentially be carried out without (time) penalty.

Number three. When generating conflict clauses, MiniSat-type conflict minimisation has now become commonplace. This uses the clauses involved in the conflict to carry out self-subsuming resolution on the conflict clause generated. Just as with clause vivification, we can use our cache to carry out self-subsuming resolution with the (conceptually binary) clauses stored in the cache. This is not much different from clause vivification, but it allows us to do simplification in the middle of a restart, instead of patiently waiting for the restart to end. Furthermore, it can uncover that certain learnt clauses can become binary, thus alleviating the problem of cleaning “useless” learnt clauses that could have become binary through, e.g. clause vivification.

I am aware that all the above three could be carried out without a cache — in fact, CryptoMiniSat could do (and most of the time did) all of the above without it. The advantage of having the cache is speed: things that used to take immense amounts of time can now be done really fast. However, what interests me the most in this cache, is the new uses that will come of it. I was originally only aware of number (3), then when I realised (1), I dived deep and realised that (2) can be done. I think more uses will eventually emerge.

Transitive OTF self-subsuming resolution

SAT, ,

The title may be a bit long, but its essence is very simple: we try to shorten learnt clauses. The basic idea was described in this post: there is a clause we just derived, e.g.

d V -e V f V g (1)

where d,e,f,g are binary variables, - is binary negation, and V is the binary OR operator. We can remove a literal from this using self-subsuming resolution with e.g. the 2-long clause:

f V -g (2)

removing g from clause (1). This has been achieved before using on-the-fly self-subsuming resolution. The trick we add now is the following. Let’s assume that clause (2) was not in the clause database. With the above technique, g would not be removed. However, if clauses:

f V a
-a V -g

are inside the clause database, we could, in fact, remove g, since the above two clauses, when we resolve them on a become:

f V -g

i.e. clause (2), what we have been searching for! So, how could we do this kind of reasoning efficiently? It turns out that this is not so difficult. We simply need to try to propagate -f using only the 2-long clauses. Then, we will reach -g through the intermediary, a.

Naturally, we can do the above recursive-propagation process not only for f but for all literals in the original clause (1), and then try to perform on-the-fly self-subsuming resolution, as before. There is only one catch: doing this kind of recursive propagation on all 2-long clauses for all literals in a clause is too time-consuming. So we only do it for clauses that are short: 5 literals or shorter. The results are in, and seem to indicate that transitive on-the-fly self-subsuming resolution with a limit of 5-long clauses is indeed viable:

The set of problems used were those of the SAT Competition 2009, and the time limit was 1500 seconds on some powerful machines — they are approx 2x as fast as those used in the competition. As you can see, transitive OTF self-subsuming resolution seems to pay off in terms of number of problem instances solved within a certain time limit. I have decided to add this feature to the upcoming CryptoMiniSat 2.6.1, which should be ready soon.

Propagating faster

SAT, ,

Propagation (BCP) in SAT is the single most expensive operation. The algorithm essentially does the following:

while (queue_head < trail.size()) {
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch[p].end(); i++) {
    confl = prop_confl(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

where the function prop_confl() executes the propagation or returns a conflict, if necessary.

The problem with the above function is that clauses come in all shapes and sizes. In CryptoMiniSat, there are two kinds of clauses, normal clauses and XOR clauses. Naturally, these need to be handled differently. Furthermore, if the clause’s size is small, it is more efficient to handle it differently. The way CryptoMiniSat has done this before was to have a separate “watches” for each of these. As you can guess, this is very suboptimal.

The new code in CryptoMiniSat now uses a different approach. Instead of having a watches_normal, watches_xor, watches_binary, and a for loop for each, we have one watches and one for loop, but this time, the struct Watch encodes the type of the watched clause. So our new BCP function is:

while (queue_head < trail.size()) {
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch.end(); i++) {
    if (i->isBinary())
      confl = prop_confl_bin(i->clause);
    if (i->isNormal())
      confl = prop_confl_norm(i->clause);
    if (i->isXor())
      confl = prop_confl_xor(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

This new method reduces the jump-around that the processor otherwise would have done with all those separate for loops. It has an important drawback, though: it is now more complicated (and more expensive) to fully propagate binary clauses before any other clause. The original code had this:

while (queue_head < trail.size()) {
  bin_queue_head = queue_head;
  while(bin_queue_head < trail.size()) {
    Literal p = trail[bin_queue_head];
    vector<Watch>& thiswatch_bin = watches_bin[p];
    for (i = thiswatch_bin.begin(); i!=thiswatch_bin.end(); i++) {
      confl = prop_confl_bin(i->clause);
      if (confl != NULL) return confl;
    }
    bin_queue_head++;
  }
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch.end(); i++) {
    confl = prop_confl(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

Since there are no separate watchlists for binary clauses anymore, we are required to go through all clauses all the time in the first for loop, or we can simply skip the first loop. The disadvantage of this is that some variables could have possibly been set by binary clauses may now be set by non-binary clauses, which leads to a possibly increased number of literals in the resulting learnt clause — since the incoming arcs into the conflict will likely contain more clauses that are larger than 2-long.