Tag Archives: glues

Machine Learning and SAT

Development, Research, SAT, ,

I have lately been digging myself into a deep hole with machine learning. While doing that it occurred to me that the SAT community has essentially been trying to imitate some of ML in a somewhat poor way. Let me explain.

CryptoMiniSat and clause cleaning strategy selection

When CryptoMiniSat won the SAT Race of 2010, it was in large part because I realized that glucose at the time was essentially unable to solve cryptographic problems. I devised a system where I could detect which problems were cryptographic. It checked the activity stability of variables and if they were more stable than a threshold, it was decided that the problem was cryptographic. Cryptographic problems were then solved using a geometric restart strategy with clause activities for learnt database cleaning. Without this hack, it would have been impossible to win the competition.
Continue reading →

A note on learnt clauses

Research, SAT, , , , ,

Learnt clauses are clauses derived while searching for a solution with a SAT solver in a CNF. They are at the heart of every modern so-called “CDCL” or “Conflict-Driven Clause-Learning” SAT solver. SAT solver writers make a very important difference between learnt and original clauses. In this blog post I’ll talk a little bit about this distinction, why it is important to make it, and why we might want to relax that distinction in the future.

A bit of terminology

First, let me call “learnt” clauses “reducible” and original clauses “irreducible”. This terminology was invented by Armin Biere I believe, and it is conceptually very important.

If a clause is irreducible it means that if I remove that clause from the clause database and solve the remaining system of constraints, I might end up with a solution that is not a solution to the original problem. However, these clauses might not be the “original” clauses — they might have been shortened, changed, or otherwise manipulated such as through equivalent literal replacement, strengthening, etc.

Reducible clauses on the other hand are clauses that I can freely remove from the clause database without the risk of finding a solution that doesn’t satisfy the original set of constraints. These clauses could be called “learnt” but strictly speaking they might not have been learnt through the 1st UIP learning process. They could have been added through hyper-binary resolution, they could have been 1UIP clauses that have been shortened/changed, or clauses obtained through other means such as Gaussian Elimination or other high-level methods.

The distinction

Reducible clauses are typically handled “without care” in a SAT solver. For example, during bounded variable elimination (BVE) resolutions are not carried out with reducible clauses. Only irreducible clauses are resolved with each other and are added back to the clause database. This means that during variable elimination information is lost. For this reason, when bounded variable addition (BVA) is carried out, one would not count the simplification obtained through the removal of reducible clauses, as BVE could then completely undo BVA. Naturally, the heuristics in both of these systems only count irreducible clauses.

Reducible clauses are also regularly removed or ‘cleaned’ from the clause database. The heuristics to perform this has been a hot topic in the past years and continue to be a very interesting research problem. In particular, the solver Glucose has won multiple competitions by mostly tuning this heuristic. Reducible clauses need to be cleaned from the clause database so that they won’t slow the solver down too much. Although they represent information, if too many of them are present, propagation speed grinds to a near-halt. A balance must be achieved, and the balance lately has shifted much towards the “clean as much as possible” side — we only need to observe the percentage of clauses cleaned between MiniSat and recent Glucose to confirm this.

An observation about glues

Glues (used first by Glucose) are an interesting heuristic in that they are static in a certain way: they never degrade. Once a clause achieves glue status 2 (the lowest, and best), it can never loose this status. This is not true of dynamic heuristics such as clause activities (MiniSat) or other usability metrics (CryptoMiniSat 3). They are highly dynamic and will delete a clause eventually if it fails to perform well after a while. This makes a big difference: with glues, some reducible clauses will never be deleted from the clause database, as they have achieved a high enough status that most new clauses will have a lower status (a higher glue) and will be deleted instead in the next cleaning run.

Since Glucose doesn’t perform variable elimination (or basically any other optimization that could forcibly remove reducible clauses), some reducible clauses are essentially “locked” into the clause database, and are never removed. These reducible clauses act as if they were irreducible.

It’s also interesting to note that glues are not static: they are in fact updated. The way they are updated, however, is very particular: they can obtain a lower glue number (a higher chance of not being knocked out) through some chance encounters while propagating. So, if they are propagated often enough, they have a higher chance of obtaining a lower glue number — essentially having a higher chance to be locked into the database.

Some speculation about glues

What if these reducible clauses that are locked into the clause database are an important ingredient in giving glues the edge? In other words, what if it’s not only the actual glue number that is so wildly good at guessing the usefulness of a reducible clause, instead the fact that their calculation method doesn’t allow some reducible clauses ever to be removed also significantly helps?

To me, this sounds like a possibility. While searching and performing conflict analysis SAT solvers are essentially building a chain of lemmas, a proof. In a sense, constantly removing reducible clauses is like building a house and then knocking a good number of bricks out every once in a while. If those bricks are at the foundation of the system, what’s above might collapse. If there are however reducible clauses that are never “knocked out”, they can act as a strong foundation. Of course, it’s a good idea to be able to predict what is a good foundation, and I believe glues are good at that (though I think there could be other, maybe better measures invented). However, the fact that some of them are never removed may also play a significant role in their success.

Locking clauses

Bounded variable addition is potentially a very strong system that could help in shortening proofs. However, due to the original heuristics of BVE it cannot be applied if the clauses it removes are only reducible. So, it can only shorten the description of the original problem (and maybe incidentally some of the reducible clauses) but not only the reducible clauses themselves. This is clearly not optimal for shortening the proof. I don’t know how lingeling performs BVA and BVE, but I wouldn’t be surprised if it has some heuristic where it treats some reducible clauses as irreducible (thereby locking them) so that it could leverage the compression function of BVA over the field of reducible clauses.

Unfortunately, lingeling code is hard to read, and it’s proprietary code so I’d rather not read it unless some licensing problems turn up. No other SAT solver performs BVA as an in-processing method (riss performs it only as pre-processing, though it is capable to perform BVA as in-processing), so I’m left on my own to guess this and code it accordingly.

UPDATE: According to Norbert Manthey lingeling doesn’t perform BVA at all. This is more than a little surprising.

End notes

I believe it was first Vegard Nossum who put into my head the idea of locking some reducible clauses into the database. It only occurred to me later that glues automatically achieve that, and furthermore, they seem to automatically lock oft-propagated reducible clauses.

There are some problems with the above logic, though. I believe lingeling increments the glue counter of some (all?) reducible clauses on a regular basis, and lingeling is a good solver. That would defeat the above logic, though the precise way glues are incremented (and the way they are cleaned) in lingeling is not entirely clear to me. So some of the above could still hold. Furthermore, lingeling could be so well-performing for other reasons — there are more to SAT solvers than just search and resolution. Lately, up to 50% or more of the time spent in modern SAT solvers could be used to perform actions other than search.

Clause glues are a mystery to me

Development, SAT, , ,

Note: the work below has been done in collaboration with Vegard Nossum, but the wording and some of the (mis-)conculsions are mine. If you are interested, check out his master thesis, it’s quite incredible

Anyone who has ever tried to really understand clause glues in SAT solvers have probably wondered what they really mean. Their definition is simple: the number of variables in the final conflict clause that come from different decision levels. An explanation of these terms can be found here. On the surface, this sounds very simple and clean: the number of different decision levels should somehow be connected to the number of variables that need to be set before the learnt clause activates itself, i.e. it causes a propagation or a conflict. Unfortunately, this is just the surface, because if you try to draw 2-3 implication graphs, you will see that in fact the gap between the number of variables needed to be set (let’s call this ‘activation number’) and the glue can be virtually anything, making the glue a potentially bad indicator of the activation number.

The original reasoning

The original reasoning behind glues is the following: variables in the same decision level, called ‘blocks of variables’ have a chance to be linked together through direct dependencies, and these dependencies should be expressed somehow in order to reduce the number of decisions needed to reach a conflict (and thus ultimately reduce the search space). To me, this reasoning is less clear than the one above. In fact, there are about as many intuitions about glues as the number of people I have met.

Glucosetrack

With Vegard Nossum we have developed (in exactly one day) something quite fun. On the face of it, it’s just glucose 1.0, plain and simple. However, it has an option, “-track”, which does the following: whenever a learnt clause is about to cause a conflict, it jumps over this learnt clause, saves the state of the solver, and works on until the next conflict in order to measure the amount of work the SAT solver would have had to do if that particular learnt clause had not been there. Then, when the next clause wishes to cause a conflict, it records the amount of propagation and decisions between the original conflict and this new conflict, resets the state to the place saved, and continues on its journey as if nothing had happened. The fun part here is that the state is completely reset, meaning that the solver behaves exactly as glucose, but at the same time it records how much search that particular cause has saved. This is very advantageous because it doesn’t give some magical number like glue, but actually measures the usefulness of the given clause. Here is a typical output:

c This is glucose 1.0  with usefulness tracking by
c Vegard Nossum and Mate Soos. Based on glucose, which
c is in run based on MiniSat, Many thanks to all teams
c
c ============================[ Problem Statistics ]=============================
c |                                                                             |
c |  Number of variables:  138309                                               |
c |  Number of clauses:    942285                                               |
c |  Parsing time:         0.28         s                                       |
============================[ Search Statistics ]==============================
| Conflicts |          ORIGINAL         |          LEARNT          | Progress |
|           |    Vars  Clauses Literals |    Limit  Clauses Lit/Cl |          |
===============================================================================
|         0 |  138309   942285  2636352 |   314095        0   -nan |  0.000 % |
|       620 |  138074   942285  2636352 |   314095      615     82 |  1.559 % |
|       919 |  135307   925938  2596895 |   314095      906     75 |  3.908 % |
|      2714 |  130594   894562  2518954 |   314095     2664     67 |  6.799 % |
|      2814 |  130593   894562  2518954 |   314095     2763     69 |  6.808 % |
|      2930 |  130592   894562  2518954 |   314095     2879     70 |  6.808 % |
|      4042 |  127772   874934  2471045 |   314095     3974     69 |  9.292 % |
|      4142 |  127772   874934  2471045 |   314095     4074     70 |  9.292 % |
...
c Cleaning clauses (clean number 0). Current Clause usefulness stats:
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(0 , 961074 , 107 , 5 , 42 , 185509 , 1301341 , 0);
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(0 , 944729 , 14 , 1 , 7 , 36865 , 268229 , 0);
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(0 , 948275 , 7 , 1 , 15 , 27909 , 220837 , 0);
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(0 , 953762 , 102 , 2 , 2 , 29365 , 197410 , 0);
...
c End of this round of database cleaning
...
|     38778 |  110896   758105  2182915 |   314095    28270     93 | 20.167 % |
|     39488 |  110894   758105  2182915 |   314095    28978     93 | 20.185 % |
c Cleaning clauses (clean number 1). Current Clause usefulness stats:
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(1 , 979236 , 71 , 1 , 8 , 45531 , 280156 , 0);
INSERT INTO data(cleanno, idx, size, glue, conflicts, props, bogoprops, decisions) VALUES(1 , 954908 , 2 , 2 , 7 , 0 , 232760 , 0);
...

The output is in SQL format for easy SQL import. The “size” is the clause size, “glue” is the glue number, “conflicts” is the number of times the clause caused a conflict, “props” is the number of propagations gained by having that clause (i.e. by doing the conflict early), “bogoprops” is an approximation of the amount of time gained based on the number of watchlists and the type of clauses visited during propagation, and “decisions” is the number of decisions gained. The list is sorted according to “bogoprops”, though once the output is imported to MySQL, many sortings are possible. You might notice that the ‘glue’ is 1 for some clauses (e.g. on the second output line) — these are clauses that have caused a propagation at decision level 0, so they will eventually be removed through clause-cleaning, since they are satisfied. Notice that high up, there are some relatively large clauses (of size 102 for example) with glue 2, that gain quite a lot in terms of time of search. The gained conflicts/propagations/etc. are all cleared after every clause-cleaning, though since clauses are uniquely indexed (‘idx’), they can be accumulated in all sorts of ways.

The program is 2-5x slower than normal glucose, but considering that it has to save an extreme amount of state due to the watchlists being so difficult to handle and clauses changing all the time, I think it does the job quite well — as a research tool it’s certainly quite usable. In case you wish to download it, it’s up in GIT here, and you can download a source tarball here. To build, issue “cmake .” and “make”. Note that the tool only measures the amount of search saved by having the clause around when it tries to conflict. It does not measure the usefulness of the propagations that a learnt clause makes. Also, it doesn’t measure the other side of the coin: the (potentially better) conflict generated by using this clause instead of the other one. In other words, it gives a one-sided view (no measure of help through propagation) of a one-sided view (doesn’t measure the quality of difference between the conflict clauses generated). Oh well, it was a one-day hack.

Experiments

I have made very few experiments with glucosetrack, but you might be interested in the following result. I have taken UTI-20-10p0, ran it until completion, imported the output into MySQL, and executed the following two queries. The first one:

SELECT glue, AVG(props), FROM data
WHERE glue >= 2 AND size >= 2
GROUP BY glue
ORDER BY glue

calculates the average number of saved propagations between each round of cleaning for clauses of glue >= 2 (i.e. clauses that didn’t eventually cause a propagation at decision level 0), and of size >= 2, because unitary clauses are of no interest. The second is very similar:

SELECT size, AVG(props), FROM data
WHERE glue >= 2 AND size >= 2
GROUP BY size
ORDER BY size

which calculates the same as above, but for size.

Some explanation is in order here regarding why I didn’t count SUM(), and instead opted for AVG(). In fact I personally did make graphs for SUM(), but Vegard corrected me: there is in fact no point in doing that. If I came up with a new glue calculation function that gave an output of ‘1’ for every clause, then the SUM for that function would look perfect: every clause would be in the same bracket, saving a lot of propagations, but that would not help me make a choice of which clauses to throw out. But the point of glues is exactly that: to help me decide which clauses to throw out. So what we really want is a usefulness metric that tells me that if I keep clauses in that bracket, how much do I gain per clause. The AVG() gives me that.

Here goes the AVG() graph for the last clause cleaning (clause cleaning iteration 33):

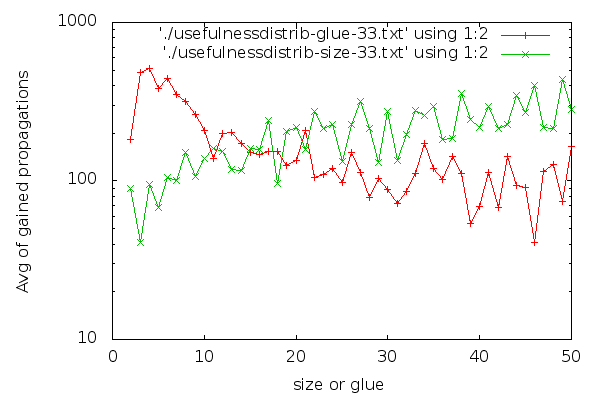
Notice that the y axis is in logscale. In case you are interested in a larger graph, here it is. The graph for clause cleaning iteration 22 is:

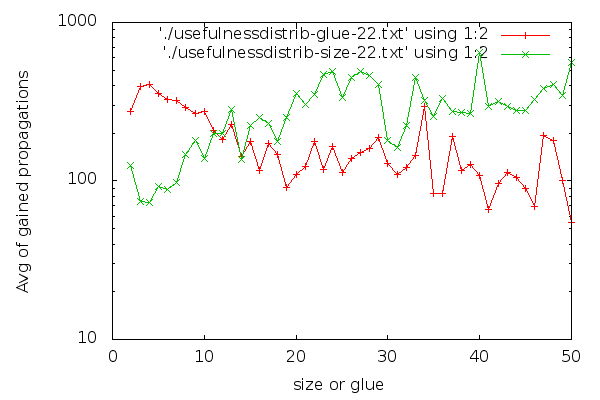(Iteration 11 has high fluctuations due to less data, but for the interested, here it is). I think it’s visible that glues are good distinguishers. The graph for glues drops down early and stays low. For sizes, the graph is harder to read. Strangely, short clauses are not that good, and longer clauses are better on average. If I had to make a choice about which clauses to keep based on the size graph, it would be a hard choice to make: I would be having trouble selecting a group that is clearly better than the rest. There are no odd-one-out groups. On the other hand, it’s easier to characterise which clauses are good to have in terms of glues: take the low glue ones, preferably below 10, though we can skip the very low ones if we are really picky. An interesting side-effect of the inverse inclination of the size and glue graphs and the fact that “glue<=size” is that maybe we could choose better clauses to keep if we go for larger clauses that have a low glue.

Conclusions

Unfortunately, there are no real conclusions to this post. I guess running glucosetrack for far more than just one example, and somehow also making it measure the difference between the final conflict clauses’ effectiveness would help to write some partially useful conclusion. Vegard and me have tried to put some time and effort into this, but to not much avail I am afraid.

PS: Notice that glucosetrack allows you to generate many of the graphs here using the right SQL query.

Extended resolution is working!

SAT, ,

The subtitle of this post should really say: and I was wrong, again. First, let me explain what I have been wrong about — wrong assumptions are always the most instructive.

I have been convinced for the past year that it’s best to have two type of restart and corresponding learnt clause usefulness strategies: the glue-based restart&garbage collection of Glucose and a variation of the geometric restart and activity-based garbage collection of MiniSat. The glue-based variation was observed to be very good for industrial instances with many variables, many of which can be fixed easily, and the MiniSat-type variation was observed to be good for cryptography-type instances with typically low number of variables, almost none of which can be fixed. However, I had the chance to talk to Armin Biere a couple of weeks ago, and while talking with him, I have realised that maybe one of Lingeling’s advantages was its very interesting single restart strategy, based on agility (presentation, PDF) which seemed to let it use glue-based garbage collection all the time, succeeding to solve both types of instances. So, inspired by the CCC crowd, in only 10 minutes I have implemented a simple version of this restart strategy into CryptoMiniSat, and voilá, it seems to work on both type of instances, using only glues!

Now that this dumb assumption of mine is out of the way, let me talk about what is really interesting. As per my last post, I have managed to add a lightweight form of Extended Resolution (ER). Since then, I have improved the heuristics here-and-there, and I have launched the solver on a somewhat strange problem (aloul-chnl11-13.cnf) that only has 2×130 variables, but seems to be hard: very few SAT solvers were able to solve this instance within 10000 secs during the last SAT Competition. So, after CryptoMiniSat cutting the problem into two distinct parts, each containing 130 variables, it started adding variables to better express the learnt clauses… and the average learnt clause size dropped from ~30 literals to ~13 literals in comparison with the version that didn’t add variables. Furthermore, and this is the really interesting part, the solver was able to prove that some of these newly introduced variables must have a certain value, or that some of them were equi- or antivalent to others. So, after lightening the problem up to contain ~3000 variables, the solver was able to solve it in less than 5 minutes. This is, by the way, a problem that neither the newest MiniSat, nor Lingeling, nor Glucose can solve. Interestingly, the Extended Resolution version of Glucose can solve it, in almost the same time as CryptoMiniSat with ER added…