In SAT solvers, removing unneeded learnt clauses from the clause database sounds like a trivial task: we somehow determine which clauses are not needed and we call remove() on them. However, in case performance is an issue, it can get a bit more more complicated.

The problem

The issue at hand is that clauses are stored in two places: as a list of pointers to the clauses and in a list of lists called the watchlist. Removing clauses from either list can be an operation if we e.g. remove every element from the list, one by one. In fact, an old version of the most popular SAT solver, MiniSat2, used to do exactly this:

sort(learnts, reduceDB_lt());
for (i = j = 0; i < learnts.size() / 2; i++){ if (learnts[i]->size() > 2 && !locked(*learnts[i]))
        removeClause(*learnts[i]);
    else
        learnts[j++] = learnts[i];
}
[...]

Here, removeClause() is called on each clause individually, where removeClause() eventually calls remove() twice, where remove() is a linear operation:

template
static inline void remove(V& ts, const T& t)
{
    int j = 0;
    for (; j < (int)ts.size() && ts[j] != t; j++);
    assert(j < (int)ts.size());
    for (; j < (int)ts.size()-1; j++) ts[j] = ts[j+1];
    ts.pop();
}

It is clear that if the number of learnt clauses removed is a significant percent of all clauses (which it is after some runtime), this is an operation.

My original solution

My original solution to this problem was the following. First, I did a sweep on the watchlist and detached all learnt clauses. This is an 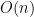operation. Then, I ran the algorithm above, without the removeClause(). Finally, I attached the remaining learnt clauses: again an 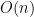operation. This solution is significantly faster than the MiniSat one as its worst-case runtime is only 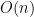. The improvement is measurable — worst-case cleaning times dropped from seconds to tenths of seconds. However, it can be further improved.

The improved solution

The improvement that came to my mind just yesterday was the following. I can keep a one bit marker in each learnt clause that indicates whether the clause needs to be detached or not. Then, I can run the algorithm as above but replace removeClause() with markclause() and run through the watchlists once to remove (and free) the marked clauses. This works really well and it only necessitates one sweep of the watchlists, without any useless detach+reattach cycles.

The newer GitHub version of MiniSat also marks the clauses instead of detaching them immediately and then removes them in one sweep, later. Interestingly, it keeps a list of ‘dirty’ occurrence lists and only goes through the ones that need removal. I find that a bit strange for this specific purpose: usually almost all watchlists are affected. In other cases, though, keeping dirty lists in mind can be a good idea, e.g. if only few clauses are removed for some optimization step.