Tag Archives: self-subsuming resolution

A note on learnt clauses

Research, SAT, , , , ,

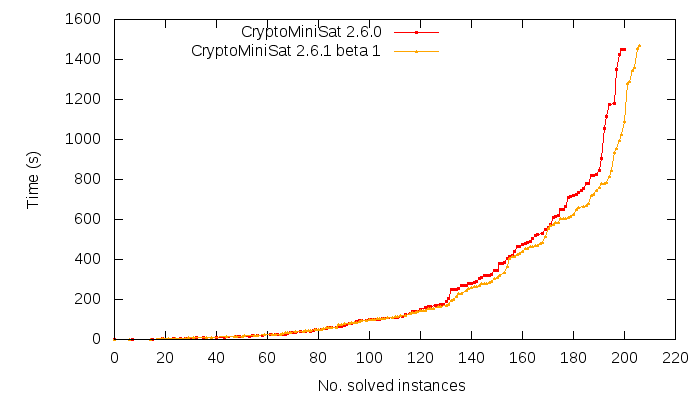
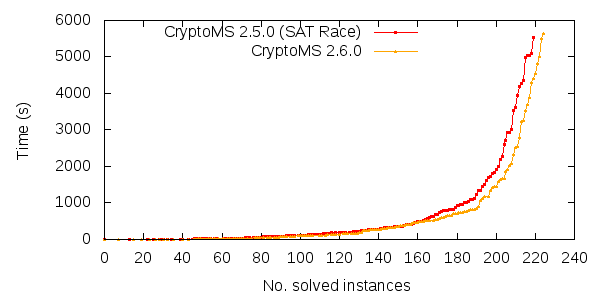
Learnt clauses are clauses derived while searching for a solution with a SAT solver in a CNF. They are at the heart of every modern so-called “CDCL” or “Conflict-Driven Clause-Learning” SAT solver. SAT solver writers make a very important difference between learnt and original clauses. In this blog post I’ll talk a little bit about this distinction, why it is important to make it, and why we might want to relax that distinction in the future.

A bit of terminology

First, let me call “learnt” clauses “reducible” and original clauses “irreducible”. This terminology was invented by Armin Biere I believe, and it is conceptually very important.

If a clause is irreducible it means that if I remove that clause from the clause database and solve the remaining system of constraints, I might end up with a solution that is not a solution to the original problem. However, these clauses might not be the “original” clauses — they might have been shortened, changed, or otherwise manipulated such as through equivalent literal replacement, strengthening, etc.

Reducible clauses on the other hand are clauses that I can freely remove from the clause database without the risk of finding a solution that doesn’t satisfy the original set of constraints. These clauses could be called “learnt” but strictly speaking they might not have been learnt through the 1st UIP learning process. They could have been added through hyper-binary resolution, they could have been 1UIP clauses that have been shortened/changed, or clauses obtained through other means such as Gaussian Elimination or other high-level methods.

The distinction

Reducible clauses are typically handled “without care” in a SAT solver. For example, during bounded variable elimination (BVE) resolutions are not carried out with reducible clauses. Only irreducible clauses are resolved with each other and are added back to the clause database. This means that during variable elimination information is lost. For this reason, when bounded variable addition (BVA) is carried out, one would not count the simplification obtained through the removal of reducible clauses, as BVE could then completely undo BVA. Naturally, the heuristics in both of these systems only count irreducible clauses.

Reducible clauses are also regularly removed or ‘cleaned’ from the clause database. The heuristics to perform this has been a hot topic in the past years and continue to be a very interesting research problem. In particular, the solver Glucose has won multiple competitions by mostly tuning this heuristic. Reducible clauses need to be cleaned from the clause database so that they won’t slow the solver down too much. Although they represent information, if too many of them are present, propagation speed grinds to a near-halt. A balance must be achieved, and the balance lately has shifted much towards the “clean as much as possible” side — we only need to observe the percentage of clauses cleaned between MiniSat and recent Glucose to confirm this.

An observation about glues

Glues (used first by Glucose) are an interesting heuristic in that they are static in a certain way: they never degrade. Once a clause achieves glue status 2 (the lowest, and best), it can never loose this status. This is not true of dynamic heuristics such as clause activities (MiniSat) or other usability metrics (CryptoMiniSat 3). They are highly dynamic and will delete a clause eventually if it fails to perform well after a while. This makes a big difference: with glues, some reducible clauses will never be deleted from the clause database, as they have achieved a high enough status that most new clauses will have a lower status (a higher glue) and will be deleted instead in the next cleaning run.

Since Glucose doesn’t perform variable elimination (or basically any other optimization that could forcibly remove reducible clauses), some reducible clauses are essentially “locked” into the clause database, and are never removed. These reducible clauses act as if they were irreducible.

It’s also interesting to note that glues are not static: they are in fact updated. The way they are updated, however, is very particular: they can obtain a lower glue number (a higher chance of not being knocked out) through some chance encounters while propagating. So, if they are propagated often enough, they have a higher chance of obtaining a lower glue number — essentially having a higher chance to be locked into the database.

Some speculation about glues

What if these reducible clauses that are locked into the clause database are an important ingredient in giving glues the edge? In other words, what if it’s not only the actual glue number that is so wildly good at guessing the usefulness of a reducible clause, instead the fact that their calculation method doesn’t allow some reducible clauses ever to be removed also significantly helps?

To me, this sounds like a possibility. While searching and performing conflict analysis SAT solvers are essentially building a chain of lemmas, a proof. In a sense, constantly removing reducible clauses is like building a house and then knocking a good number of bricks out every once in a while. If those bricks are at the foundation of the system, what’s above might collapse. If there are however reducible clauses that are never “knocked out”, they can act as a strong foundation. Of course, it’s a good idea to be able to predict what is a good foundation, and I believe glues are good at that (though I think there could be other, maybe better measures invented). However, the fact that some of them are never removed may also play a significant role in their success.

Locking clauses

Bounded variable addition is potentially a very strong system that could help in shortening proofs. However, due to the original heuristics of BVE it cannot be applied if the clauses it removes are only reducible. So, it can only shorten the description of the original problem (and maybe incidentally some of the reducible clauses) but not only the reducible clauses themselves. This is clearly not optimal for shortening the proof. I don’t know how lingeling performs BVA and BVE, but I wouldn’t be surprised if it has some heuristic where it treats some reducible clauses as irreducible (thereby locking them) so that it could leverage the compression function of BVA over the field of reducible clauses.

Unfortunately, lingeling code is hard to read, and it’s proprietary code so I’d rather not read it unless some licensing problems turn up. No other SAT solver performs BVA as an in-processing method (riss performs it only as pre-processing, though it is capable to perform BVA as in-processing), so I’m left on my own to guess this and code it accordingly.

UPDATE: According to Norbert Manthey lingeling doesn’t perform BVA at all. This is more than a little surprising.

End notes

I believe it was first Vegard Nossum who put into my head the idea of locking some reducible clauses into the database. It only occurred to me later that glues automatically achieve that, and furthermore, they seem to automatically lock oft-propagated reducible clauses.

There are some problems with the above logic, though. I believe lingeling increments the glue counter of some (all?) reducible clauses on a regular basis, and lingeling is a good solver. That would defeat the above logic, though the precise way glues are incremented (and the way they are cleaned) in lingeling is not entirely clear to me. So some of the above could still hold. Furthermore, lingeling could be so well-performing for other reasons — there are more to SAT solvers than just search and resolution. Lately, up to 50% or more of the time spent in modern SAT solvers could be used to perform actions other than search.

Caching

SAT, , ,

“Representation is the essence of programming”
Frederic P. Brooks Jr., “The Mythical Man-month”

Looking through the literature on SAT solvers, it is rare to find any algorithm that uses a form of time-memory trade-off. In fact, it is rare to find any algorithm that uses too much memory. This also shows up in practice, as it’s rare to find a SAT solver using too much memory. This translates to the following: if a SAT solver can in an effective way utilize the typically abundant memory, that SAT solver will have an advantage. Based on this logic, I think CryptoMiniSat is doing good.

What I have realised is that it’s great to know all the literals we can reach from any given literal. Let me explain. Let’s say we have a look at literal “v1”, i.e. “v1 = true”. We propagate this literal as usual, and we reach a set of literals that are implied. For example, we reach “v2, v3, -v4”. This knowledge is regularly computed by modern SAT solvers, but is also quickly thrown away. I advocate keeping this, and here is why. There are a number of very interesting things we can do with these, three of which I have found useful.

Number one. This is the best, and the least obvious one. The algorithm used for computing equivalent literals (i.e. “v1 = -v2” or “v1 = v4”) is a variation of Tarjan’s algorithm for finding strongly connected components (SCC). This algorithm requires a set of binary clauses such as “-v1 v2” and “v1 -v2” as input to find equivalent literals, in the example case “v1 = -v2”. The most obvious way to “feed” this algorithm with information is to give it all the binary clauses we have. But that misses out on all the binary clauses that are not directly apparent in the problem, but  could be derived from the problem. For example, if “-v1 -v4” was not directly in the problem, SCC cannot find the equivalence “v1 = v4”. Naturally, by using our cache, we can be sure that “-v1 -v4” is part of the problem (since “v1” propagates “-v4”). So, using this cache, we can substantially increase the power of SCC. More equivalent literals lead to less variables, and an overall faster solving.

Number two. Clause vivification is a method to make the original clauses of the problem shorter. It’s a relatively simple algorithm that enqueues the literals in the clauses one-by-one and checks if their propagation leads to a conflict. If so, then the clause can be shortened. With the cache, we can do something similar, though less powerful in terms of reasoning power, but far more effective in terms of speed. The trick is to simply try every single literal in the clause: if a literal propagates the inverse of another literal in the clause, we can remove it. For example, if the clause is “a b -c”, and in the cache for “b” there is “f,g,h,j,-c”, then we know that conceptually there exists a clause “-b -c”, which means we can now remove “b” from the original clause, using the the self-subsuming resolution rule. This form of vivification is, although technically less strong than normal vivification, is typically 50-100x faster than normal vivification and is almost as powerful. This kind of speed advantage means it can essentially be carried out without (time) penalty.

Number three. When generating conflict clauses, MiniSat-type conflict minimisation has now become commonplace. This uses the clauses involved in the conflict to carry out self-subsuming resolution on the conflict clause generated. Just as with clause vivification, we can use our cache to carry out self-subsuming resolution with the (conceptually binary) clauses stored in the cache. This is not much different from clause vivification, but it allows us to do simplification in the middle of a restart, instead of patiently waiting for the restart to end. Furthermore, it can uncover that certain learnt clauses can become binary, thus alleviating the problem of cleaning “useless” learnt clauses that could have become binary through, e.g. clause vivification.

I am aware that all the above three could be carried out without a cache — in fact, CryptoMiniSat could do (and most of the time did) all of the above without it. The advantage of having the cache is speed: things that used to take immense amounts of time can now be done really fast. However, what interests me the most in this cache, is the new uses that will come of it. I was originally only aware of number (3), then when I realised (1), I dived deep and realised that (2) can be done. I think more uses will eventually emerge.

Transitive OTF self-subsuming resolution

SAT, ,

The title may be a bit long, but its essence is very simple: we try to shorten learnt clauses. The basic idea was described in this post: there is a clause we just derived, e.g.

d V -e V f V g (1)

where d,e,f,g are binary variables, - is binary negation, and V is the binary OR operator. We can remove a literal from this using self-subsuming resolution with e.g. the 2-long clause:

f V -g (2)

removing g from clause (1). This has been achieved before using on-the-fly self-subsuming resolution. The trick we add now is the following. Let’s assume that clause (2) was not in the clause database. With the above technique, g would not be removed. However, if clauses:

f V a
-a V -g

are inside the clause database, we could, in fact, remove g, since the above two clauses, when we resolve them on a become:

f V -g

i.e. clause (2), what we have been searching for! So, how could we do this kind of reasoning efficiently? It turns out that this is not so difficult. We simply need to try to propagate -f using only the 2-long clauses. Then, we will reach -g through the intermediary, a.

Naturally, we can do the above recursive-propagation process not only for f but for all literals in the original clause (1), and then try to perform on-the-fly self-subsuming resolution, as before. There is only one catch: doing this kind of recursive propagation on all 2-long clauses for all literals in a clause is too time-consuming. So we only do it for clauses that are short: 5 literals or shorter. The results are in, and seem to indicate that transitive on-the-fly self-subsuming resolution with a limit of 5-long clauses is indeed viable:

The set of problems used were those of the SAT Competition 2009, and the time limit was 1500 seconds on some powerful machines — they are approx 2x as fast as those used in the competition. As you can see, transitive OTF self-subsuming resolution seems to pay off in terms of number of problem instances solved within a certain time limit. I have decided to add this feature to the upcoming CryptoMiniSat 2.6.1, which should be ready soon.

CryptoMiniSat 2.6.0 released

SAT, ,

Version 2.6.0 of the CryptoMiniSat SAT solver has been released. The new release incorporates a number of important additions and discoveries. Additions include a better memory manager and better watchlists, while the discoveries include an interesting use of asymmetric branching and an on-the-fly self-subsuming resolution algorithm.

The new solver can now solve 221 problems from the SAT Competition of 2009 within the same timing&CPU constraints, while the 2.5.0 (i.e. SAT Race) version could only solve 217. Here is a comparison plot:

The cut-off for the competition for these machines was approx at 5000 sec. As can be seen from the graph (which goes until 6000 sec), the new solver does even better in the longer run:  the additions seem to improve the long-term behaviour.

As for the future, I think there is still a lot of things to do. For example, the solver still doesn’t have blocked clause elimination, which could help, and it is still missing some ideas that others have published. Notably, it doesn’t do on-the-fly subsumption at every step of the conflict generation process, only at the very last step. In case you are interested to add any of these in a transparent manner, feel free to hack away at the git repository.

Edited to Add (3/09/2010): The performance of CryptoMiniSat on the SAT Race 2010 problems has also changed with the new version. The new CryptoMiniSat can now solve 75 problems (instead of 74) within the time limit. More importantly, the average time to solve these 75 instances has decreased considerably, to around 111 seconds per instance (from 138 s/inst), which is very close to the results of lingeling, an extremely fast and very advanced solver. There is still a lot to be learnt from lingeling, however: its memory footprint is far smaller, and its preprocessing techniques in some areas are much better than that of CryptoMiniSat.

On-the-fly self-subsuming resolution

SAT, ,

I have recently been trying a new method of shortening learnt clauses. There is a learnt clause minimisation paper by Sörensson and Biere, and I have recently been trying to do more. The trick I use, is that many literals can be removed from learnt clauses, if self-subsuming resolution (see my older post) is applied to them.

During self-subsuming resolution, under normal circumstances, the clauses used to remove literals with are the short clauses: binary and tertiary clauses. The trick I have discovered, is that since CryptoMiniSat keeps binary and tertiary clauses natively inside the watchlists (see my previous post), so doing self-subsuming resolution can be done extremely fast. We simply need to put the literals of the newly learnt clause into a fast-addressable memory, then go through the watchlists of every literal in the clause, and remove the literals that match.

The code used to achieve this is the following:

for (uint32_t i = 0; i < cl.size(); i++) seen[cl[i].toInt()] = 1;
for (Lit *l = cl.getData(), *end = cl.getDataEnd(); l != end; l++) {
    if (seen[l->toInt()] == 0) continue;

    Lit lit = *l;
    //watched is messed: lit is in watched[~lit]
    vec& ws = watches[(~lit).toInt()];
    for (Watched* i = ws.getData(), *end = ws.getDataEnd(); i != end; i++) {
        if (i->isBinary()) {
            if (seen[(~i->getOtherLit()).toInt()]) {
                seen[(~i->getOtherLit()).toInt()] = 0;
            }
        }
    }
}

Lit *i = cl.getData();
Lit *j= i;
for (Lit* end = cl.getDataEnd(); i != end; i++) {
    if (seen[i->toInt()]) *j++ = *i;
    seen[i->toInt()] = 0;
}
cl.shrink(i-j);

Essentially, we set the seen vector (which is initially all 0), to 1 where the original clause contained a literal. Then, we go through the watchlists, and check if any binary clause could strengthen the clause. If so, we unset the corresponding bit in seen. Finally, we clean the clause from the literals where seen is 0 (and then set all parts of seen back to 0).

The actual implementation only differs from the one above by also using tertiary clauses (which are also natively inside the watchlists) to do self-subsuming resolution. The results are very promising: CryptoMiniSat can now solve 2 more problems from the 2009 SAT Competition instances within the original time limit, and seems to scale better in the longer run, too. An example statistics output of CryptoMiniSat (from the UTI-20-10p1 problem):

c OTF cl watch-shrink   : 961191      (0.64      clauses/conflict)
c OTF cl watch-sh-lit   : 6096451     (6.34       lits/clause)

which means that in 64% of the cases, on-the-fly self-subsuming resolution was useful, and on average, it removed 6.3 literals from each clause where it was useful.