Tag Archives: Grain of Salt

Fun facts about SAT solving (part 1)

July 1, 2011Research, SATGrain of Salt, research, resolutionmsoos

Last time I gave a talk, I got some quite deserved fire about the way I approach SAT solving: in a more practical than scientific way. So, to give some food for thought for those who wish to approach SAT from a more scientific viewpoint, and to demonstrate to what lengths I have gone to give (at least to myself) a scientific viewpoint, let me talk a little bit about a fun fact that I have found. The fun fact, as is quite usual for SAT, seems entirely trivial, even banal, but has somehow (so far) eluded proper explanation for me. Maybe you will be the one to give the right explanation :)

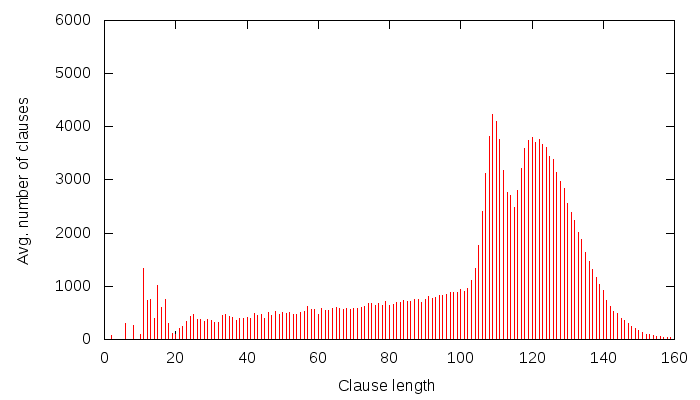
So, I generate a Grain cipher instance using, e.g. the Grain-of-Salt tool that I developed. If you don’t want to generate these yourself, there are a couple (multi-hundred thousand) pre-generated such problems you can download from here. I launch MiniSat 2.1 “core”(i.e. the most simple version) on these problems with a little twist: I write to a file the length of each generated learnt clause. Now, there are two kinds of CNF files I use: one that has 60 randomly picked randomly set state variables, and another one that is plain, and doesn’t have any variables set. Obviously, the CNF that has variables set should be easier to solve, and if Grain is a proper cipher, it should be about 2^60 easer to solve. Now, I print the average learnt clause length that I observe for the CNF that has 0 variables set, and I get this graph:

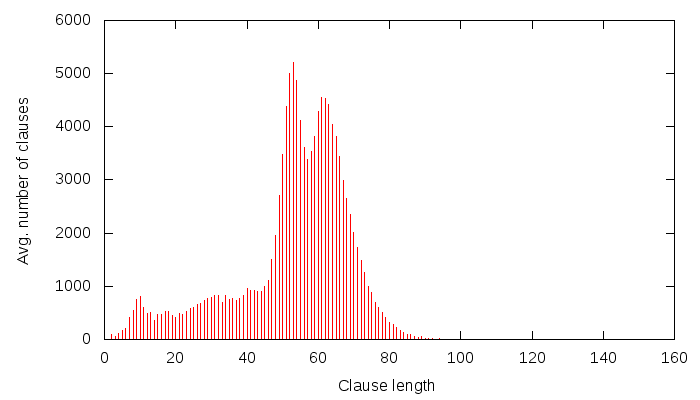
I am sure one could sing long and elaborate songs about this graph, but instead, I will just say: it has a strange curvy thing at around clause length 120. Now, I will generate a similar graph, but this time, I will use a CNF that has 60 state (i.e. important) variables set. Note that this should indeed be 2^60 times easier to solve (since Grain is a nice cipher, and my CNF generation abilities aren’t that poor). So the same graph for this CNF looks like this:

All right. This one, as I am sure you have noticed, has a curvy thing at around 60. Using elementary math, 120-60 = 60. Right, so one could reason: well, there were X unknowns, I have set 60 of them, now there are only X-60 left, so the average clause length should be 60 less! That I think doesn’t explain much, if anything, however. First off, the number of unknowns were in fact 160 — that’s the unknown state of Grain that we were trying to solve. Second, the learnt clauses don’t only contain state variables… in fact, a lot of variables they contain are not state variables at all! Furthermore, why should the 1st UIP scheme be so exact about clause sizes? After all, it’s just a graph-analysis algorithm working at the local conflict — it has no clue about the problem it is working with, much less about the number of state bits set in our instance of Grain.

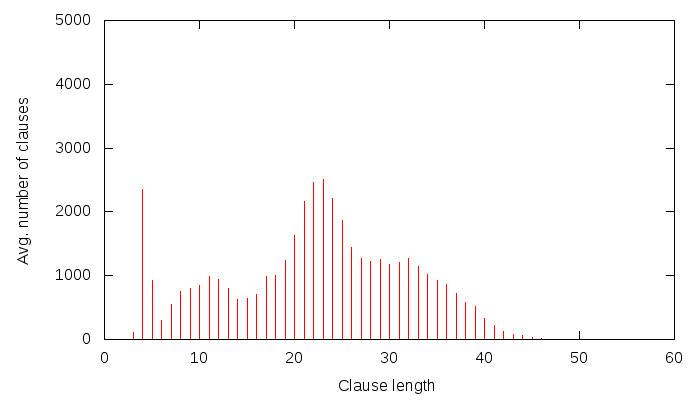
One could say that this is just a dumb example, and it has no real meaning. Maybe I just stumbled upon it, after all, 120/2 = 60, etc. However, this doesn’t seem to be the case. I can, in fact, reproduce this for a lot of X’s for any of the following ciphers: Grain, Trivium, Bivium, HiTag2 and Crypto-1. Let me show one from HiTag2. Again, we are solving for the state, and we don’t set any state bits (i.e. this is the full HiTag2 problem):

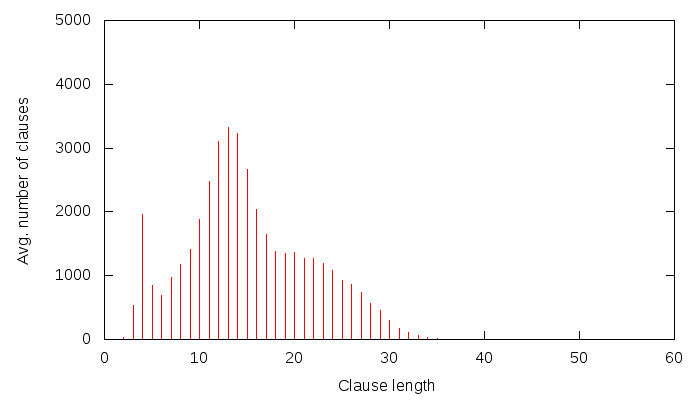
Okay, there is a bumpy thing at around 23. Now, let’s set 10 randomly picked state variables to random values, and run the example again:

There seems to be a bumpy thing at around 13. 23-10 = 13. That’s about right.

By the way, I have stumbled upon the above fun fact about 2 years ago (well before CryptoMiniSat was born), when working on my diploma thesis — these graphs are actually taken verbatim from my thesis. I have worked a lot on SAT in the past 2 years, but this has been haunting me ever since. Maybe someone could explain it to me?

PS: Does anyone know if someone has done an in-depth analysis of learnt clause length distributions, maybe even three-dimensional, showing the time on the Z axis? It would be awesome to do that, if it hasn’t been done yet!

ANF to CNF conversion

July 6, 2010SATANF, CNF, Grain of Salt, Sagemsoos

Algebraic Normal Form, or simply ANF, is the form used to describe cryptographic functions. It looks like this:
$a*b \oplus b*c \oplus b \oplus d = 0\\b*c \oplus c \oplus a = 0\\\ldots$
Where $a,\ldots d$ are binary variables, the $\oplus$ sign is binary XOR, and the $*$ sign is binary AND. Every item that is connected with the XOR-s is called a monomial, and its degree is the number of independent variables inside it. So, $a*b$ is a 2-degree monomial in the first equation, and $c$ is a 1-degree monomial in the second equation.

An important problem in SAT is to translate an ANF into the input of SAT solvers, Conjunctive Normal Form, or simply CNF. A CNF formula looks like this:
$a \vee b \vee c = 1\\a \vee \neg d = 1\\\ldots$
Where again $a,\ldots d$ are binary variables, the $\vee$ sign is the binary OR, and the $\neg$ sign is the binary NOT (i.e. inverse).

The scientific reference paper

The most quoted article about ANF-to-CNF translation is that by Courtois and Bard, which advocates for the following translation process:

Introduce internal variables for every monomial of degree larger than 1
Describe the equations as large XORs using the recently introduced variables

The example problem in CNF

According to the original method, the equations presented above are first translated to the following form:
$v1 = a*b\\v2 = b*c\\v1 \oplus v2 \oplus b \oplus d = 0\\v2 \oplus c \oplus a = 0$

Where $v1, v2$ are fresh binary variables. Then, each of the above equations are translated to CNF. The internal variables are translated as such:

Translation of $v1 = a*b$ :
$v1 \vee \neg a \vee \neg b = 1\\\neg v1 \vee a = 1\\\neg 1 \vee b = 1$
Translation of $v2 = b*c$
$v2 \vee \neg b \vee \neg c = 1\\\neg v2 \vee b = 1\\\neg v2 \vee c = 1$
Translation of $v1 + v2 + b + d = 0$ :
$\neg v1 \vee v2 \vee b \vee d = 1\\v1 \vee \neg v2 \vee b \vee d = 1\\v1 \vee v2 \vee \neg b \vee d = 1\\v1 \vee v2 \vee b \vee -d = 1\\\neg v1 \vee \neg v2 \vee \neg b \vee d = 1\\\neg v1 \vee \neg v2 \vee b \vee \neg d = 1\\\neg v1 \vee v2 \vee \neg b \vee \neg d = 1\\v1 \vee \neg v2 \vee \neg b \vee \neg d = 1$
Translation of $v2 + c + a = 0$ :
$v2 \vee c \vee \neg a = 1\\v2 \vee \neg c \vee a = 1\\\neg v2 \vee c \vee a = 1\\\neg v2 \vee \neg c \vee \neg a = 1$

We are now done. The final CNF file is this. This final CNF has a small header, and some fluffs have been removed: variables are not named, but referred to with a number, and the = true-s have been replaced with a line-ending 0.

As you can imagine, there are many ways to enhance this process. I have written a set of them down in this paper. The set of improvements in a nutshell are the following:

If a variable’s value is given, (e.g. a = true), first substitute this value in the ANF, and transcribe the resulting ANF to CNF.
If there are two monomials, such as: a*b + b in an equation, make a non-standard monomial (-a)*b from the two, and transcribe this to CNF. Since the CNF can use negations, this reduces the size of the resulting CNF
If the ANF can be described using Karnaugh maps shorter than with the method presented above, use that translation method.

An automated way

I just got a nice script to perform step (1) from Martin Albrecht, one of the developers of Sage:

sage: B = BooleanPolynomialRing(4500,'x')
sage: L = [B.random_element(degree=2,terms=10) 
      for _ in range(4000)]
sage: s = [B.gen(i) + GF(2).random_element() 
      for i in range(1000)]
sage: %time F = 
      mq.MPolynomialSystem(L+s).
      eliminate_linear_variables(maxlength=1)
CPU time: 1.03 s,  Wall time: 1.11 s

In this code, Martin generates a boolean system of equations with 4500 variables, with 4000 random equations each with randomly selected monomials of degree 2 and of XOR size 10. Then, he sets 1000 random variables to a random value (true or false), and finally, he substitutes the assigned values, and simplifies the system. If you think this is a trivial issue, alas, it is not. Both Maple and Sage take hours to perform it if using the standard eval function. The function above uses a variation of the ElimLin algorithm from the Courtois-Bard paper to do this efficiently.

Gaussian elimination is released

May 9, 2010SATGaussian elimination, Grain of Salt, Releasemsoos

The new CryptoMiniSat, version 2.4.2 now has on-the-fly Gaussian elimination compiled in by default. You can simply use it by issuing e.g.

./cryptominisat --gaussuntil=100 trivium-cipher.cnf

and enjoy outputs such as:
c gauss unit truths : 0 c gauss called : 31323 c gauss conflicts : 5893 (18.81 %) c gauss propagations : 7823 (24.98 %) c gauss useful : 43.79 % c conflicts : 34186 (4073.39 / sec) c decisions : 39715 (6.86 % random)
Which basically tells that gaussian elimination was called 31 thousand times out of 39 thousand, and so it was essentially running almost all the time. Out of the 31’323 times it was called, 44% of the cases it found either a conflict or a propagation. This is a very good result, and is typical of the Trivium cipher. Trivium can be speeded up by up to 2x with Gaussian elimination. I will put up lots of CNFs, so you will be able to play around with them and (optionally) verify these results.

The magic parameter “–gaussuntil=100” tells the program to execute Gaussian elimination until decision level 100, and no deeper. I haven’t implemented and automation into finding the best depth, and so I use this (very) crude fixed number 100. Probably better results could be achieved with a fine tuning of the depth cut-off, but I don’t have the time for the moment to play around with it. However, if you are interested, you will be able to try out different depths, different ciphers, etc. I will shortly be releasing a tool called “Grain of Salt” to generate CNFs for any shift-register based stream cipher, so you can test them against CryptoMiniSat or any other SAT solver.

I hope you will enjoy using on-the-fly Gaussian elimination in CryptoMiniSat 2.4.2!

Wonderings of a SAT geek

A blog about SAT solving and cryptography