CryptoMiniSat 2.6.0 released

SAT, ,

Version 2.6.0 of the CryptoMiniSat SAT solver has been released. The new release incorporates a number of important additions and discoveries. Additions include a better memory manager and better watchlists, while the discoveries include an interesting use of asymmetric branching and an on-the-fly self-subsuming resolution algorithm.

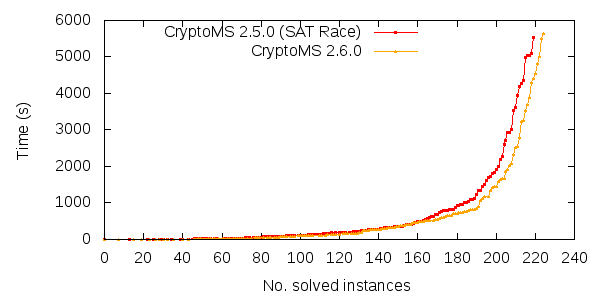
The new solver can now solve 221 problems from the SAT Competition of 2009 within the same timing&CPU constraints, while the 2.5.0 (i.e. SAT Race) version could only solve 217. Here is a comparison plot:

The cut-off for the competition for these machines was approx at 5000 sec. As can be seen from the graph (which goes until 6000 sec), the new solver does even better in the longer run:  the additions seem to improve the long-term behaviour.

As for the future, I think there is still a lot of things to do. For example, the solver still doesn’t have blocked clause elimination, which could help, and it is still missing some ideas that others have published. Notably, it doesn’t do on-the-fly subsumption at every step of the conflict generation process, only at the very last step. In case you are interested to add any of these in a transparent manner, feel free to hack away at the git repository.

Edited to Add (3/09/2010): The performance of CryptoMiniSat on the SAT Race 2010 problems has also changed with the new version. The new CryptoMiniSat can now solve 75 problems (instead of 74) within the time limit. More importantly, the average time to solve these 75 instances has decreased considerably, to around 111 seconds per instance (from 138 s/inst), which is very close to the results of lingeling, an extremely fast and very advanced solver. There is still a lot to be learnt from lingeling, however: its memory footprint is far smaller, and its preprocessing techniques in some areas are much better than that of CryptoMiniSat.

On-the-fly self-subsuming resolution

SAT, ,

I have recently been trying a new method of shortening learnt clauses. There is a learnt clause minimisation paper by Sörensson and Biere, and I have recently been trying to do more. The trick I use, is that many literals can be removed from learnt clauses, if self-subsuming resolution (see my older post) is applied to them.

During self-subsuming resolution, under normal circumstances, the clauses used to remove literals with are the short clauses: binary and tertiary clauses. The trick I have discovered, is that since CryptoMiniSat keeps binary and tertiary clauses natively inside the watchlists (see my previous post), so doing self-subsuming resolution can be done extremely fast. We simply need to put the literals of the newly learnt clause into a fast-addressable memory, then go through the watchlists of every literal in the clause, and remove the literals that match.

The code used to achieve this is the following:

for (uint32_t i = 0; i < cl.size(); i++) seen[cl[i].toInt()] = 1;
for (Lit *l = cl.getData(), *end = cl.getDataEnd(); l != end; l++) {
    if (seen[l->toInt()] == 0) continue;

    Lit lit = *l;
    //watched is messed: lit is in watched[~lit]
    vec& ws = watches[(~lit).toInt()];
    for (Watched* i = ws.getData(), *end = ws.getDataEnd(); i != end; i++) {
        if (i->isBinary()) {
            if (seen[(~i->getOtherLit()).toInt()]) {
                seen[(~i->getOtherLit()).toInt()] = 0;
            }
        }
    }
}

Lit *i = cl.getData();
Lit *j= i;
for (Lit* end = cl.getDataEnd(); i != end; i++) {
    if (seen[i->toInt()]) *j++ = *i;
    seen[i->toInt()] = 0;
}
cl.shrink(i-j);

Essentially, we set the seen vector (which is initially all 0), to 1 where the original clause contained a literal. Then, we go through the watchlists, and check if any binary clause could strengthen the clause. If so, we unset the corresponding bit in seen. Finally, we clean the clause from the literals where seen is 0 (and then set all parts of seen back to 0).

The actual implementation only differs from the one above by also using tertiary clauses (which are also natively inside the watchlists) to do self-subsuming resolution. The results are very promising: CryptoMiniSat can now solve 2 more problems from the 2009 SAT Competition instances within the original time limit, and seems to scale better in the longer run, too. An example statistics output of CryptoMiniSat (from the UTI-20-10p1 problem):

c OTF cl watch-shrink   : 961191      (0.64      clauses/conflict)
c OTF cl watch-sh-lit   : 6096451     (6.34       lits/clause)

which means that in 64% of the cases, on-the-fly self-subsuming resolution was useful, and on average, it removed 6.3 literals from each clause where it was useful.

Self-subsuming resolution

SAT, , ,

Self-subsuming resolution in SAT uses the resolution operator to carry out its magic. Resolution can be used on two clauses if they share a variable, but the sign of the variable is inverted, e.g.
v1 V v2
-v1 V v3 V v4
(where v1..v4 are binary variables and “V” means binary OR) can be resolved on v1, producing the clause:
v2 V v3 V v4

In SAT this is used to simplify problems as follows. Let’s assume we have many clauses, among which there are these three:
a V c (1)
a V -c V d V f (2)
a V -c V g (3)
In this case, if we use the resolution operator on (1) and (2), we get:
a V d V f (4)
The interesting thing about (4) is that it is a strict subset of (2). In other words, we could simply replace (2) with (4), thus shortening clause (2). If we use the resolution operator on (1) and (3) we get:
a V g (5)
whose literals form a strict subset of those of (3), so we can replace (3) with (5), again shortening a clause. We shortened 2 clauses, each with one literal. For completeness, this technique can be applied in a recursive manner on all possible clause-pairs.

Until now, CryptoMiniSat was doing self-subsuming resolution in such a way that the clauses being manipulated were kept inside the propagation queue. The problem was, that the propagation queue enforces a very strict position of literals in the clause. So, when e.g. removing literal “a” from clause (3), CryptoMiniSat had to completely remove the clause, and then to completely re-add it, since the position of “a” changed (it got removed). The additional overhead for this was simply too much: in certain cases, self-subsuming resolution took 130 seconds to complete, 115 of which was taken by this detach-reattach overhead.

The solution to this problem was to completely remove all clauses from the propagation queue, then do self-subsuming resolution, and finally re-add the clauses. Interestingly, complete removal of all clauses is very fast (essentially, a constant-time operation, even though removing clauses one-by-one is very costly), and completely re-adding them is also very fast (linear in the number of clauses). The first impressions from this technique are very positive, and I decided to release CryptoMiniSat 2.6.0 with this technique included.

NOTE: Thanks to N. Sörensson for pointing me out that self-subsuming resolution could be done better. I am not sure this is what he meant, but fingers are crossed.

Asymmetric branching

SAT,

Asymmetric branching is an algorithm that shortens CNF clauses in SAT Solvers. A clause, for instance v1 V v2 V v3 V v4 (where letters are binary variables and V represents binary OR) could possibly be shortened to v1 V v2 V v3. To find out if it can be, all we have to do is to put -v1,-v2 and -v3 into the propagation queue and then propagate. If we receive a conflict from the propagation engine, we can learn the clause v1 V v2 V v3, which (incidentally, though this was the point), subsumes the original clause, so we can simply remove variable v4 from the original clause.

Ok, so much for theory. Now comes the hard part: how do we do this such that it actually speeds up the solving? The problem is that asymmetric branching, when done on all possible clauses, is slow. However, its benefits could be large, since a shortened clause naturally leads a faster propagation and shorter resolution proofs thus less propagation need.

I have been experimenting in getting some benefit from asymmetric branching, and now it works extremely well for CryptoMiniSat. The trick I use, is that I first sort the clauses according to size, and only try to shorten with asymmetric branching the top couple of clauses. This ensures that the largest clauses are shortened first. Since the largest clauses contribute most the to size of the resolution proof and they are the slowest to propagate, this makes sense.

CryptoMiniSat tries to do asymmetric branching regularly, always for only a little while (~2 seconds). I believe this is useful, because as the amount of time the program has been trying to solve a problem increases, it makes sense that we have a bit more time to do things that could help resolve the problem faster. For instance, if CryptoMiniSat has been trying to solve a given problem for 30 minutes unsuccessfully with the standard clause-learning DPLL procedure in vain, we can allocate 2-3 seconds to possibly gain ~5-10% later. In the example case it can be assumed that since we haven’t been able to solve it for 30 minutes, probably we won’t solve it in the next 10 minutes, so gaining 5% on 10 minutes is 30 seconds, far more than the 2-3 seconds we invested.

The results with asymmetric branching with CryptoMiniSat are quite astounding. Using the 2009 SAT Competition benchmark set with an approximately correct timeout, CryptoMiniSat could normally solve 217 problems. With asymmetric branching, CryptoMiniSat can now solve 220 — a huge increase: last year, 16 solvers running in parallel could only solve 229 instances in total.

Edited to add (26/09/2010): Clause Vivification by Piette, Hamadi and Sais is a paper about the above described method, though with a number of key differences. The paper seems to advocate for a complete procedure, furthermore, it calls the conflict generation routine in certain cases. I believe that the above described way of carrying out this technique brings more tangible benefits, especially for larger problems.

(Updated: we need to branch on the inverse of the clause’s literals. Thanks to Vegard Nossum for spotting this)

Propagating faster

SAT, ,

Propagation (BCP) in SAT is the single most expensive operation. The algorithm essentially does the following:

while (queue_head < trail.size()) {
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch[p].end(); i++) {
    confl = prop_confl(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

where the function prop_confl() executes the propagation or returns a conflict, if necessary.

The problem with the above function is that clauses come in all shapes and sizes. In CryptoMiniSat, there are two kinds of clauses, normal clauses and XOR clauses. Naturally, these need to be handled differently. Furthermore, if the clause’s size is small, it is more efficient to handle it differently. The way CryptoMiniSat has done this before was to have a separate “watches” for each of these. As you can guess, this is very suboptimal.

The new code in CryptoMiniSat now uses a different approach. Instead of having a watches_normal, watches_xor, watches_binary, and a for loop for each, we have one watches and one for loop, but this time, the struct Watch encodes the type of the watched clause. So our new BCP function is:

while (queue_head < trail.size()) {
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch.end(); i++) {
    if (i->isBinary())
      confl = prop_confl_bin(i->clause);
    if (i->isNormal())
      confl = prop_confl_norm(i->clause);
    if (i->isXor())
      confl = prop_confl_xor(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

This new method reduces the jump-around that the processor otherwise would have done with all those separate for loops. It has an important drawback, though: it is now more complicated (and more expensive) to fully propagate binary clauses before any other clause. The original code had this:

while (queue_head < trail.size()) {
  bin_queue_head = queue_head;
  while(bin_queue_head < trail.size()) {
    Literal p = trail[bin_queue_head];
    vector<Watch>& thiswatch_bin = watches_bin[p];
    for (i = thiswatch_bin.begin(); i!=thiswatch_bin.end(); i++) {
      confl = prop_confl_bin(i->clause);
      if (confl != NULL) return confl;
    }
    bin_queue_head++;
  }
  Literal p = trail[queue_head];
  vector<Watch>& thiswatch = watches[p];
  for (i = thiswatch.begin(); i!=thiswatch.end(); i++) {
    confl = prop_confl(i->clause);
    if (confl != NULL) return confl;
  }
  queue_head++;
}

Since there are no separate watchlists for binary clauses anymore, we are required to go through all clauses all the time in the first for loop, or we can simply skip the first loop. The disadvantage of this is that some variables could have possibly been set by binary clauses may now be set by non-binary clauses, which leads to a possibly increased number of literals in the resulting learnt clause — since the incoming arcs into the conflict will likely contain more clauses that are larger than 2-long.