Category Archives: Research

Research-related information

Collecting solver data

Research, SAT, ,

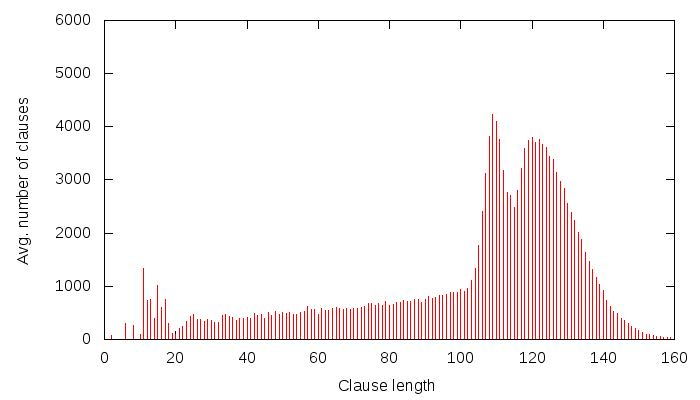
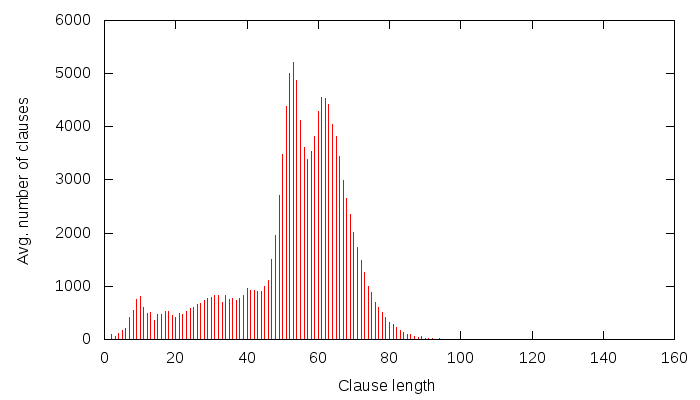
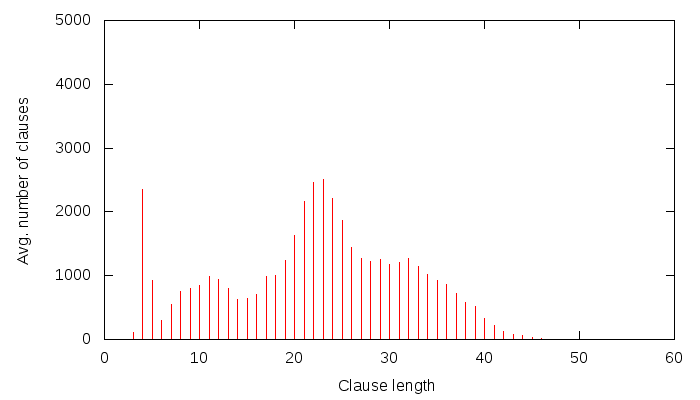
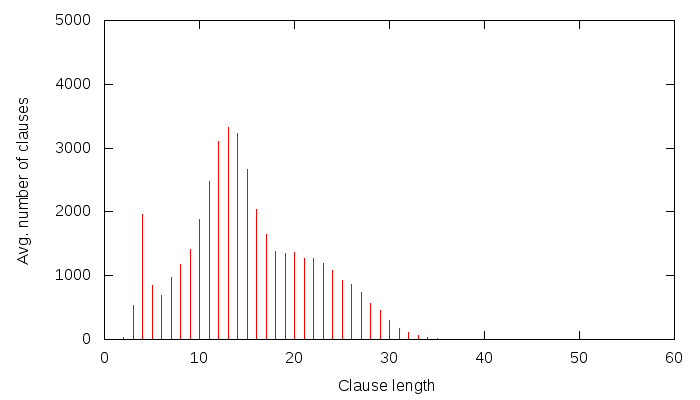
Lately, I have been putting a lot of effort into collecting data about solver behaviour and dumping it on-the-fly to a MySQL database. Some of this data is then presented by a PHP&javascript interface, such as this.The goal is to better understand how solving works, and thus to possibly come up with better strategies for solving. The requirements of the data gathered are: speed to calculate, size to store and usefulness.

Gathered data

There are some obvious statistics that one would like to collect, such as number of conflicts, propagations and conflicts per second, etc — these are all gathered by almost every SAT solver out there. However, it would be interesting to have more. Here is what CryptoMiniSat now gathers and dumps using highly efficient prepared bulk insert statements, using at most 5% of time.

For each variable, dumped once in a while:

  • no. times propagated false, and true (separately)
  • no. times decided false and true (sep.)
  • no. times flipped polarity
  • avg & variance of decision level
  • avg & variance of propagation level

For each clause larger than 3-long, dumped once in a while:

  • activity
  • conflict at which it was introduced (if learnt)
  • number of propagations made
  • number of conflicts made
  • number of times any of its literal was looked at during BCP
  • number of times it was looked at (dereferenced) during BCP
  • number of times used to resolve with during learnt clause generation
  • number of resolutions needed to during its generation (if learnt clause)

For earch restart:

  • no. of reducible&irreducible (i.e. learnt&non-learnt) binary clauses
  • no. of red&irred tertiary clauses (separately)
  • no. of red&irred long clauses (sep)
  • avg, variance,  min and max of learnt clause glues
  • avg, var, min, max of learnt clause sizes
  • avg, var, min, max of number of resolutions for 1st UIP
  • avg,var,min,max of branch depths
  • avg,var,min,max of backjump length –in the number of literals unassigned
  • avg,var,min,max of backjump lenght — in the number of levels backjumped
  • avg, var, min, max times a conflict followed a conflict without decisions being made
  • avg,var,min,max of agility
  • no. of propagations by red&irred binary clauses
  • no. of props by red&irred tertiary clauses
  • no. of props by red&irred long clauses
  • no. of conflicts by red&irred binary clauses (separately)
  • no. of conflicts by red&irred tertiary clauses (sep)
  • no. of conflicts by red&irred  long clauses (sep)
  • no. of learnt unit, binary, tertiary, and long clauses (sep)
  • avg,var, min,max of watchlist size traversed during BCP
  • time spent
  • no. of decisions
  • no. of propagations
  • no. of variables flipped
  • no. of variables set positive&negative (sep)
  • no. of variables currently unset
  • no. of variables currently replaced
  • no. of variables currently eliminated
  • no. of variables currently set

For each learnt clause database cleaning:

  • for reducible clauses removed: all the data in the “clauses larger than 3-long” data above, summed up
  • for reducible clauses not removed: all the data in the “clauses larger than 3-long” data above, summed up
  • no. of clauses removed
  • no. of clauses not removed
  • for all irred clauses (these are not touched): all the data in the “clauses larger than 3-long” data above, summed up

For every N conflicts:

  • clause size distribution
  • clause glue distribution
  • clause size and glue scatter data

This is all, and is not all mine. Suggestions were made by many, some as much as a year ago: George Katsirelos, Luca Melette, Vegard Nossum, Valentin-Mayer Eichberger, Ben Schlabs,  Said Jabbour and Niklas Sörensson. Naturally, none of these people necessarily approve of how I gather data or what I do with the data gathered, but they helped, so listing them is only fair.

What’s not yet or cannot be gathered

Two suggestions are still on the TODO list:

  • counting the number of conflicts done while a learnt clause was “locked”, i.e. has propagated in the current search tree. This stat of a learnt clause could tell us if the clause seemed essential to the search or not. If a clause propagated once, at the bottom of the search tree, and then the variable propagated was quickly unset, it’s not the same as if the same clause propagated at the top of the search tree, and then the variable it set was essentially never unset.
  • for each variable, counting the number of conflicts done while the variable was set. This is interesting, because if a variable was propagated only once, at top-level, it will seem like it was never set (set only once), yet it may have had a huge influence on the search tree and consequently on the learnt clauses.

Both of these require a change in the algorithm used to backjump and although I am a bit worried about the performance, I will add these soon.

Unfortunately, the data about variables can’t really be dumped so often, because it’s huge for large problems with millions of variables. So I guess I will only dump that for the most active N variables, for some sane definition of “active”. Similarly, the data about individual clauses is not dumped, only in a summed-up way during database cleaning.

Suggestions?

In case you have any ideas what else could be interesting to dump, please put it as a comment. The idea is to dump data that is cheap to compute and cheap to dump yet would be interesting for some reason or another. I am prepared to add stuff to datastructures, as you have probably guessed from the above. Yes, it makes the clause database less space-efficient, and so increases cache-miss. But on large problems, it’s going to be a cache-miss most of the time anyway, and a cache-fetch brings in 128B of data, which should be plenty for both the stats and the clause. Similarly with variables. So, don’t refrain from suggesting some stuff that takes space. Also, weird stuff is interesting. The most weird stat on the list above is definitely the “conflict after a conflict without decisions” (suggested by Said Jabbour) which I would have guessed to be zero, or near-zero, yet is pretty high, in the 30+% range.

Suggestions are welcome!

On hyper-binary resolution

Research, SAT, ,

Hyper-binary resolution is actually quite straightforward, or at least appears to be. Let’s take the following example. The clauses in our database are the following:

-a V b
-a V c
-b V -c V g
-b V -c V d
-d V g

Let’s set a to true, and see what happens. Immediately, b and c get set to true through binary clauses. If we now propagate g through the clause -b V -c V g, we ought to do hyper-binary resolution straight away, and add the clause -a V g — some call this lazy hyper-binary resolution. Good, one more binary clause!

But then… So now we have nothing to propagate using only binary clauses, we have to propagate using a long clause, -b V -c V d. As good citizens, we also do (lazy) hyper-binary resolution, coming up with the clause -a V d. Good, one more binary clause! One slight glitch now… d propagates to g, using a binary clause. But this means that setting a can propagate to g without -a V g, the first hyper-binary clause we added! So the first hyper-binary clause we added is in fact useless, it needs to be removed. If we applied transitive reduction, it would remove the first hyper-binary clause -a V g automatically.

Let’s go a bit deeper here. How could we have avoided adding the first hyper-binary clause? The obvious answer is: we should have started with -b V -c V d instead of -b V -c V g. But how easy would have it been to know (i.e. calculate) that starting with that different long clause would have made our work easier? I am not sure it would have been easy to know. And of course the example above is very trivial. It could be made much-much more complicated: g could have been reached with any number of hyper-binary resolutions from d — so simple binary look-ahead would not have helped.

I am stuck here. Any ideas?

CCC Camp’11

Personal, Research, , , ,

In case you’ve missed it, the CCC Camp was a great opportunity to meet people both working in security and otherwise. I have even met a very kind Taiwanese researcher who worked on SAT and Gröbner basis: in fact, if you haven’t had the chance to read this paper, I highly recommend it. A set of kind Taiwanese researchers recommended this paper to me, and I think it’s the most interesting SAT paper I have read in the past year.

We at SRLabs have made two releases during this camp, one that breaks GPRS encryption, and one that breaks smart card ROM encryption. I was involved with the first release, essentially working on the crypto part. In case you are interested in the videos, the one on GPRS is uploaded here, and the one on smart card ROM encryption is here. This reminds me of something: the videos from the MIT SAT/SMT Summer School are missing :( Well, given my fail there, maybe that’s a good thing :)

Note to self: higher level autarkies

Research, SAT, , ,

While reading this thesis, I have had a thought about autarkies. Let me first define what an autarky in SAT solving is:

A partial assignment phi is called a weak autarky for F if “phi*F is a subset of F” holds, while phi is an autarky for F if phi is a weak autarky for all sub-clause-sets F' of F. (Handbook of Satisfiability, p. 355)

What does this mean? Well, it means that in the clause-set {x V y, x} the assignment y=False is a weak autarky, because assigning y to False will lead to a clause that is already in the clause set (the clause x), while the assignment of x=True is a (normal) autarky, because it will satisfy all clauses that x is in. The point of autarkies is that we can remove clauses from the clause set by assigning values to a set of variables, while not changing the (un)satisfiability property of the original problem. In other words, autarkies are a cheap way of reducing the problem size. The only problem is that it seems to be relatively expensive to search for them, so conflict-driven SAT solvers don’t normally search for them (but, some lookahead solvers such as march by Marijn Heule do).

So, what is the idea? Well, I think we can have autarkies for equivalent literals, too. Here is an example CNF:

 a V d V -f
-b V d V -f
-a V e
 b V e

setting a = -b will not change the satisfiability of the problem.

We can add any number of clause pairs of the form X V Y where Y is any set of literals not in {a, -a, b, -b}, and X is (-)a in clause 1 and (-)b in clause 2. Further, one of the two variables, say, a can be in any clauses at will (in any literal form), though variable b can then only be in clauses defined by the clause pairs. Example:

 a V  d V -f
-b V  d V -f
-a V  e
 b V  e
 a V  c V -h
 a V -f

An extension that is pretty simple from here, is that we can even have clauses whose Y part is somewhat different: some literals can be missing, though again in a controlled way. For example:

 a V d
-b V d V -f
-a V e
 b V e

is possible. It would restrict b a bit more than necessary, but if a is the only one of the pairs missing literals, we are still OK I believe.

Finally, let me give an example of what these higher-level autarkies are capable of. Let’s assume we have the clause set:

 a V  d
-b V  d V -f
-a V  e
 b V  e
 a V  c V -h
 a V -f
 a V  b V  f V -g

setting a=-b now simplifies this to:

 a V  d
-a V  e
 a V  c V -h
 a V -f

which is equisatisfiable to the first one. Further, if the latter is satisfiable, computing the satisfying solution to the former given a solution to the latter is trivial.

Fun facts about SAT solving (part 1)

Research, SAT, ,

Last time I gave a talk, I got some quite deserved fire about the way I approach SAT solving: in a more practical than scientific way. So, to give some food for thought for those who wish to approach SAT from a more scientific viewpoint, and to demonstrate to what lengths I have gone to give (at least to myself) a scientific viewpoint, let me talk a little bit about a fun fact that I have found. The fun fact, as is quite usual for SAT, seems entirely trivial, even banal, but has somehow (so far) eluded proper explanation for me. Maybe you will be the one to give the right explanation :)

So, I generate a Grain cipher instance using, e.g. the Grain-of-Salt tool that I developed. If you don’t want to generate these yourself, there are a couple (multi-hundred thousand) pre-generated such problems you can download from here. I launch MiniSat 2.1 “core”(i.e. the most simple version) on these problems with a little twist: I write to a file the length of each generated learnt clause. Now, there are two kinds of CNF files I use: one that has 60 randomly picked randomly set state variables, and another one that is plain, and doesn’t have any variables set. Obviously, the CNF that has variables set should be easier to solve, and if Grain is a proper cipher, it should be about 2^60 easer to solve. Now, I print the average learnt clause length that I observe for the CNF that has 0 variables set, and I get this graph:

I am sure one could sing long and elaborate songs about this graph, but instead, I will just say: it has a strange curvy thing at around clause length 120. Now, I will generate a similar graph, but this time, I will use a CNF that has 60 state (i.e. important) variables set. Note that this should indeed be 2^60 times easier to solve (since Grain is a nice cipher, and my CNF generation abilities aren’t that poor). So the same graph for this CNF looks like this:

All right. This one, as I am sure you have noticed, has a curvy thing at around 60. Using elementary math, 120-60 = 60. Right, so one could reason: well, there were X unknowns, I have set 60 of them, now there are only X-60 left, so the average clause length should be 60 less! That I think doesn’t explain much, if anything, however. First off, the number of unknowns were in fact 160 — that’s the unknown state of Grain that we were trying to solve. Second, the learnt clauses don’t only contain state variables… in fact, a lot of variables they contain are not state variables at all! Furthermore, why should the 1st UIP scheme be so exact about clause sizes? After all, it’s just a graph-analysis algorithm working at the local conflict — it has no clue about the problem it is working with, much less about the number of state bits set in our instance of Grain.

One could say that this is just a dumb example, and it has no real meaning. Maybe I just stumbled upon it, after all, 120/2 = 60, etc. However, this doesn’t seem to be the case. I can, in fact, reproduce this for a lot of X’s for any of the following ciphers: Grain, Trivium, Bivium, HiTag2 and Crypto-1. Let me show one from HiTag2. Again, we are solving for the state, and we don’t set any state bits (i.e. this is the full HiTag2 problem):

Okay, there is a bumpy thing at around 23. Now, let’s set 10 randomly picked state variables to random values, and run the example again:

There seems to be a bumpy thing at around 13. 23-10 = 13. That’s about right.

By the way, I have stumbled upon the above fun fact about 2 years ago (well before CryptoMiniSat was born), when working on my diploma thesis — these graphs are actually taken verbatim from my thesis. I have worked a lot on SAT in the past 2 years, but this has been haunting me ever since. Maybe someone could explain it to me?

PS: Does anyone know if someone has done an in-depth analysis of learnt clause length distributions, maybe even three-dimensional, showing the time on the Z axis? It would be awesome to do that, if it hasn’t been done yet!